题目内容
已知函数f(x)=ax2+(2a+1)x+1-3a,其中a≠0.
(1)若函数y=f(x)在(-∞,2]上单调递增,求实数a的取值范围;
(2)若关于x的方程f(lgx)=0的两根之积x1•x2=10,求实数a的值.
(1)若函数y=f(x)在(-∞,2]上单调递增,求实数a的取值范围;
(2)若关于x的方程f(lgx)=0的两根之积x1•x2=10,求实数a的值.
考点:函数的零点,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:(1)由函数f(x)=ax2+(2a+1)x+1-3a在(-∞,2]上单调递增可知函数的图象开口向下且对称轴大于2;
(2)由关于x的方程f(lgx)=0的两根之积x1•x2=10可得ax2+(2a+1)x+1-3a=0的两根之和为1,从而求出a的值并验证.
(2)由关于x的方程f(lgx)=0的两根之积x1•x2=10可得ax2+(2a+1)x+1-3a=0的两根之和为1,从而求出a的值并验证.
解答:
解:(1)∵函数f(x)=ax2+(2a+1)x+1-3a在(-∞,2]上单调递增,
∴
,
解得,-
≤a<0;
(2)∵关于x的方程f(lgx)=0的两根之积x1•x2=10,
∴lgx1+lgx2=lg10=1,
即ax2+(2a+1)x+1-3a=0的两根之和为1,
则-
=1,
解得,a=-
,
经验证,成立.
∴
|
解得,-
| 1 |
| 6 |
(2)∵关于x的方程f(lgx)=0的两根之积x1•x2=10,
∴lgx1+lgx2=lg10=1,
即ax2+(2a+1)x+1-3a=0的两根之和为1,
则-
| 2a+1 |
| a |
解得,a=-
| 1 |
| 3 |
经验证,成立.
点评:本题考查了二次函数的单调性与二次函数的图象,同时考查了根与系数的关系及复合函数,属于中档题.

练习册系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程为y=
x,它的一个焦点在抛物线y2=12x的准线上,则此双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
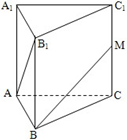 如图,已知三棱柱ABC-A1B1C1的各条棱长都相等,且CC1⊥底面ABC,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是( )
如图,已知三棱柱ABC-A1B1C1的各条棱长都相等,且CC1⊥底面ABC,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是( )