题目内容
椭圆C:
+
=1(a>b>0)过点A(1,
),离心率为
,左、右焦点分别为F1,F2,过F1的直线交椭圆于A,B两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)当△F2AB的面积为
时,求直线的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)当△F2AB的面积为
12
| ||
| 7 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)由于椭圆C:
+
=1(a>b>0)过点A(1,
),离心率为
,可得
+
=1,
=
即
=
,即可解出.
(2)对直线l的斜率分类讨论,与椭圆的方程联立可得根与系数的关系,再利用弦长公式、点到直线的距离公式、三角形的面积计算公式即可得出.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| a2 |
| 9 |
| 4b2 |
| c |
| a |
| 1 |
| 2 |
| b2 |
| a2 |
| 3 |
| 4 |
(2)对直线l的斜率分类讨论,与椭圆的方程联立可得根与系数的关系,再利用弦长公式、点到直线的距离公式、三角形的面积计算公式即可得出.
解答:
解:(1)∵椭圆C:
+
=1(a>b>0)过点A(1,
),
∴
+
=1①,
又∵离心率为
,
∴
=
,∴
=
②,
联立①②得a2=4,b2=3.
∴椭圆的方程为:
+
=1
(2)①当直线的倾斜角为
时,A(-1,
),B(-1,-
),
S△ABF2=
|AB|×|F1F2|=
×3×2≠
,不适合题意.
②当直线的倾斜角不为
时,设直线方程l:y=k(x+1),
代入
+
=1得:(4k2+3)x2+8k2x+4k2-12=0
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
,
∴|AB|=
=
=
.
点F2到直线l的距离d=
,
∴S△ABF2=
|AB|•d=
=
,
化为17k4+k2-18=0,解得k2=1,∴k=±1,
∴直线方程为:x-y+1=0或x+y+1=0.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
∴
| 1 |
| a2 |
| 9 |
| 4b2 |
又∵离心率为
| 1 |
| 2 |
∴
| c |
| a |
| 1 |
| 2 |
| b2 |
| a2 |
| 3 |
| 4 |
联立①②得a2=4,b2=3.
∴椭圆的方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(2)①当直线的倾斜角为
| π |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
S△ABF2=
| 1 |
| 2 |
| 1 |
| 2 |
12
| ||
| 7 |
②当直线的倾斜角不为
| π |
| 2 |
代入
| x2 |
| 4 |
| y2 |
| 3 |
设A(x1,y1),B(x2,y2),则x1+x2=
| -8k2 |
| 4k2+3 |
| 4k2-12 |
| 4k2+3 |
∴|AB|=
| (1+k2)[(x1+x2)2-4x1x2] |
(1+k2)[
|
| 12(1+k2) |
| 4k2+3 |
点F2到直线l的距离d=
| |k+k| | ||
|
∴S△ABF2=
| 1 |
| 2 |
12|k|
| ||
| 4k2+3 |
12
| ||
| 7 |
化为17k4+k2-18=0,解得k2=1,∴k=±1,
∴直线方程为:x-y+1=0或x+y+1=0.
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程为y=
x,它的一个焦点在抛物线y2=12x的准线上,则此双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知g(x)=1-2x,f[g(x)]=
,则f(-3)等于( )
| 1 |
| 2x+2 |
A、
| ||
B、
| ||
C、
| ||
| D、4 |
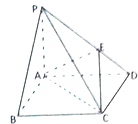 已知四棱锥P-ABCD中,PA=AB,PA⊥底面ABCD,ABCD是平行四边形,且∠BAC=90°.
已知四棱锥P-ABCD中,PA=AB,PA⊥底面ABCD,ABCD是平行四边形,且∠BAC=90°.