题目内容

先将函数f（x）=2sinxcosx的图象向左平移
π
4
个长度单位，再保持所有点的纵坐标不变横坐标压缩为原来的
1
2
，得到函数g（x）的图象，则g（x）解析式为
 
．
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：先根据二倍角公式进行化简，再由左加右减上加下减的原则可确定函数的解析式．
解答： 解：函数f（x）=2sinxcosx=sin2x，先将函数f（x）=2sinxcosx的图象向左平移
π
4
个长度单位，得到函数f（x）=sin（2x+
π
2
）=cos2x，再保持所有点的纵坐标不变横坐标压缩为原来的
1
2
，得到函数g（x）的图象，则g（x）解析式为：y=cos4x．
故答案为：y=cos4x．
点评：本题主要考查三角函数的平移．三角函数的平移原则为左加右减上加下减．
练习册系列答案
相关题目
已知函数f（x）cosx（cosx-
3
sinx）（x∈R）
（Ⅰ）写出f（x）的单调减区间；
（Ⅱ）在△ABC中，A、B、C所对的边分别是a、b、c，若f（A）=0，A∈（0，
π
2
），且（1+
3
）c=2b．求角C．
若f（x）=asin（x+
π
4
）-
6
cos（x+
π
3
），当a为何值时，函数是偶函数？何时是奇函数？
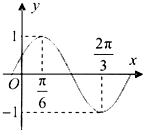已知函数f（x）=sin（ωx+φ）（ω＞0，φ＜
π
2
）的部分图象如图所示．
（Ⅰ）求函数f（x）的解析式，并写出f（x）的单调减区间；
（Ⅱ）已知△ABC的内角分别是A，B，C，角A为锐角，且f（
A
2
-
π
12
）=
1
2
，cosB=
4
5
，求sinC的值．
已知实数m≠1，函数f（x）=
2x+m，x＜2
-x-2m，x≥2
，若f（3-m）=f（1+m），则m的值为
 
．
在△ABC中，A、B、C的对边分别是a，b，c，且bcosB是acosC，ccosA的等差中项，则角B=
 
．
在锐角△ABC中，a=
2
，b=
3
，A=
π
4
，则B=
 
．
直线y=x与抛物线y=2x-x2所围成封闭图形的面积为
 
．
如图，PC切⊙O于点C，割线PAB经过圆心O，弦CD⊥AB于点E，PC=2，PB=4，则CD=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网