题目内容
若f(x)=asin(x+
)-
cos(x+
),当a为何值时,函数是偶函数?何时是奇函数?
| π |
| 4 |
| 6 |
| π |
| 3 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值,三角函数的图像与性质
分析:利用两角和公式对函数解析式化简整理,当正弦前的系数为0时,剩下的余弦函数则为偶函数;同理余弦前的系数为0时,剩下的正弦函数则为奇函数.
解答:
解:f(x)=asin(x+
)-
cos(x+
)
=
asinx+
acosx-
cosx-
sinx
=
sinx+
cosx.
∴当a=3时,f(x)=
cosx,为偶函数;
当a=
时,f(x)=
sinx,为奇函数.
| π |
| 4 |
| 6 |
| π |
| 3 |
=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
=
(
| ||||
| 2 |
| ||||
| 2 |
∴当a=3时,f(x)=
3
| ||||
| 2 |
当a=
| 3 |
| ||||
| 2 |
点评:本题主要考查了利用两角和公式对三角函数进行恒等变换,三角函数的奇偶性等问题.考查了学生的归纳和推理的能力.

练习册系列答案
相关题目
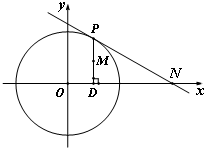 如图,在圆O:x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.设M为线段PD的中点.
如图,在圆O:x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.设M为线段PD的中点.