Question

函数f（x）=sin

π

2

x，对任意的实数t，记f（x）在[t，t+1]上的最大值为M（t），最小值为m（t），则函数
h（t）=M（t）-m（t）的值域为

 

．

Answer 1

考点：三角函数的最值

专题：计算题,函数的性质及应用,三角函数的图像与性质

分析：求出周期，画出f（x）的图象，讨论（1）当4n-1≤t≤4n，（2）当4n＜t＜4n+1，（3）当4n+1≤t≤4n+2，（4）当4n+2＜t＜4n+3，分别求出最大值和最小值，再求h（t）的值域，最后求并集即可得到．

解答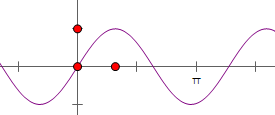： 解：函数f（x）=sin

π

2

x的周期为T=

2π

π 2

=4，
（1）当4n-1≤t≤4n，n∈Z，区间[t，t+1]为增区间，则有m（t）=sin

πt

2

，M（t）=sin

π(t+1)

2

=cos

πt

2

；
（2）当4n＜t＜4n+1，n∈Z，①若4n＜t≤4n+

1

2

，
则M（t）=1，m（t）=sin

πt

2

，
②若4n+

1

2

＜t＜4n+1，则M（t）=1，m（t）=cos

πt

2

；
（3）当4n+1≤t≤4n+2，则区间[t，t+1]为减区间，则有M（t）=sin

πt

2

，m（t）=cos

πt

2

；
（4）当4n+2＜t＜4n+3，则m（t）=-1，
①当4n+2＜t≤4n+

5

2

时，M（t）=sin

πt

2

，
②当4n+

5

2

＜t＜4n+3时，M（t）=cos

πt

2

．
则有h（t）=M（t）-m（t）
=

cos πt 2 -sin πt 2 ，4n-1≤t≤4n 1-sin πt 2 ，4n＜t≤4n+ 1 2 1-cos πt 2 ，4n+ 1 2 ＜t＜4n+1 sin πt 2 -cos πt 2 ，4n+1≤t≤4n+2 sin πt 2 +1，4n+2＜t≤4n+ 5 2 cos πt 2 +1，4n+ 5 2 ＜t＜4n+3

当4n-1≤t≤4n，h（t）的值域为[1，

2

]，
当4n＜t≤4n+

1

2

，h（t）的值域为[1-

2

2

，1），
当4n+

1

2

＜t＜4n+1，h（t）的值域为（1-

2

2

，1），
当4n+1≤t≤4n+2，h（t）的值域为[1，

2

]，
当4n+2＜t≤4n+

5

2

时，h（t）的值域为[1-

2

2

，1），
当4n+

5

2

＜t＜4n+3时，h（t）的值域为[1-

2

2

，1）．
综上，h（t）=M（t）-m（t）的值域为[1-

2

2

，

2

]．
故答案为：[1-

2

2

，

2

]．

点评：本题考查三角函数的性质和运用，考查函数的周期性和单调性及运用，考查运算能力，有一定的难度．