题目内容
10.已知△ABC中,A=30°,C=105°,b=4,则a=2$\sqrt{2}$.分析 由已知可先求B,然后结合正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$可求a的值.
解答 解:∵A=30°,C=105°,
∴B=45°
∵b=4,由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$,可得a=$\frac{bsinA}{sinB}$=$\frac{4×\frac{1}{2}}{\frac{\sqrt{2}}{2}}$=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题主要考查了正弦定理的简单应用,属于基础试题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知tanθ=-$\frac{5}{12}$,θ∈($\frac{3π}{2}$,2π),则cos(θ+$\frac{π}{4}$)=( )
| A. | $\frac{{5\sqrt{2}}}{13}$ | B. | $\frac{{7\sqrt{2}}}{13}$ | C. | $\frac{{17\sqrt{2}}}{26}$ | D. | $\frac{{7\sqrt{2}}}{26}$ |
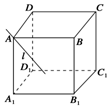 如图所示,过正方体ABCD-A1B1C1D1的顶点A作直线l,使l与棱AB,AD,AA1所成的角都相等,这样的直线l可以作4条.
如图所示,过正方体ABCD-A1B1C1D1的顶点A作直线l,使l与棱AB,AD,AA1所成的角都相等,这样的直线l可以作4条.