题目内容
定义实数a,b间的计算法则如下:a△b=
.
(1)计算2△(3△1);
(2)对x<z<y的任意实数x,y,z,判断等式x△(y△z)=(x△y)△z是否恒成立,并说明理由;
(3)写出函数y=(1△x)△x-(2△x)的解析式,其中-2≤x≤2,并求函数的值域.
|
(1)计算2△(3△1);
(2)对x<z<y的任意实数x,y,z,判断等式x△(y△z)=(x△y)△z是否恒成立,并说明理由;
(3)写出函数y=(1△x)△x-(2△x)的解析式,其中-2≤x≤2,并求函数的值域.
考点:函数解析式的求解及常用方法,函数的值域
专题:计算题
分析:(1)先求出(3△1),再求出2△(3△1)的值即可;
(2)分别求出x△(y△z)和(x△y)△z的值,判断即可;
(3)分别求出(1△x)△x和(2△x)代入求出即可.
(2)分别求出x△(y△z)和(x△y)△z的值,判断即可;
(3)分别求出(1△x)△x和(2△x)代入求出即可.
解答:
解:(1)∵(3△1)=3,
∴2△(3△1)=2△3=9;
(2)由于y>z,
∴(y△z)=y,
x△(y△z)=x△y=y2;
由于x<y,
∴(x△y)=y2,即有(x△y)△z=y2△z,
此时若y2≥z,则(x△y)△z=y2;
若y2<z,则(x△y)△z=z2.
∴等式x△(y△z)=(x△y)△z并不能保证对任意实数x,y,z都成立.
(3)由于1△x=
,2△x=2,
所以y=(1△x)-(2△x)=
,
函数的值域为[-1,2].
∴2△(3△1)=2△3=9;
(2)由于y>z,
∴(y△z)=y,
x△(y△z)=x△y=y2;
由于x<y,
∴(x△y)=y2,即有(x△y)△z=y2△z,
此时若y2≥z,则(x△y)△z=y2;
若y2<z,则(x△y)△z=z2.
∴等式x△(y△z)=(x△y)△z并不能保证对任意实数x,y,z都成立.
(3)由于1△x=
|
所以y=(1△x)-(2△x)=
|
函数的值域为[-1,2].
点评:本题考查了新定义问题,考查了函数解析式的求法,是一道中档题.

练习册系列答案
相关题目
在△ABC中,若c=2acosB,则△ABC的形状为( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、锐角三角形 |
已知某几何体的三视图如图所示,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )
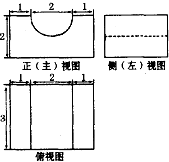

A、24-
| ||
B、24-
| ||
| C、24-π | ||
D、24-
|
以下说法正确的是( )
| A、正数的n次方根是正数 |
| B、负数的n次方根是负数 |
| C、0的n次方根是0(其中n>1且n∈N*) |
| D、负数没有n次方根 |
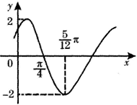 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<