题目内容

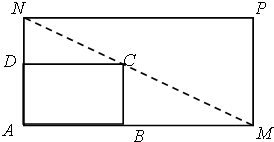如图所示，将一矩形花坛ABCD扩建为一个更大的矩形花坛AMPN，要求点B在AM上，点D在AN上，且对角线MN过点C，已知AB=3米，AD=2米，当DN的长为多少时，矩形花坛AMPN的面积最小？并求出最小值．
考点：函数模型的选择与应用
专题：应用题,函数的性质及应用,不等式的解法及应用
分析：设DN的长为x（x＞0）米，则AN=（x+2）米，表示出矩形的面积，化简矩形的面积，利用基本不等式，即可求得结论．
解答： 解：设DN的长为x（x＞0）米，则AN=（x+2）米
∵△DNC∽△NAM，∴
DN
AN
=
DC
AM
，∴AM=
3(x+2)
x

∴SAMPN=AN•AM=
3(x+2)2
x
=3x+
12
x
+12≥2
3x•
12
x
+12=24
当且仅当3x=
12
x
即x=2时，矩形花坛的面积最小为24平方米．
点评：本题考查根据题设关系列出函数关系式，考查利用基本不等式求最值，解题的关键是确定矩形的面积．
练习册系列答案
相关题目
比较下列各题中两个代数式的大小：
（1）当a＞1时，a3与a2-a+1；
（2）
2x
x2+1
与1．
若函数f（x）的定义域内存在实数x，满足f（-x）=-f（x），则称f（x）为“局部奇函数”．例如：f（x）=x2+x-1在R上存在x=1，满足f（-1）=-f（1），故称f（x）=x2+x-1为“局部奇函数”．
（1）已知二次函数f（x）=ax2+2bx-4a（a，b∈R），试判断f（x）是否为“局部奇函数”，并说明理由；
（2）设f（x）=2x+m是定义在[-1，1]上的“局部奇函数”，求实数m的取值范围．
化简：（x
1
2
y
2
3
）-3÷(x-1y-4)
1
2
+(x
a
a-b
)
1
c-a
(x
b
b-c
)
1
a-b
(x
c
c-a
)
1
b-c
．
两人约定在20：00到21：00之间相见，并且先到者必须等迟到者40分钟方可离去，如果两人出发是各自独立的，在20：00到21：00各时刻相见的可能性是相等的，求两人在约定时间内相见的概率．
已知函数f（x）=x2+2ax+1，g（x）=2x+2a（a∈R）
（1）若对任意x∈R，不等式f（x）≥
1
2
g（x）恒成立，求实数a的取值范围；
（2）设函数m（x）=
g(x)，f(x)≥g(x)
f(x)，f(x)＜g(x)
，求m（x）在x∈[2，4]上的最小值．
已知曲线C1的极坐标方程为ρ2=
2
3+cos2θ
，以极点O为原点，以极轴为x轴正向建立直角坐标系，将曲线C1上所有点的横坐标伸长到原来的2倍，纵坐标缩短到原来的
1
2
倍后得曲线C2．
（1）试写出曲线C1的直角坐标方程．
（2）在曲线C2上任取一点R，求点R到直线l：x+y-5=0的距离的最大值．
已知AB是椭圆
x2
20102
+
y2
b2
=1（2010＞b＞0）的长轴，若把该长轴2010等分，过每个等分点作AB垂线，依次交椭圆的上半部分于P1，P2，…，P2009，F1为椭圆的左焦点，则
1
2010
×（|F1A|+|F1P1|+|F1P2|+…+|F1P2009|+|F1B|）的值是
 
．
某程序框图如图所示，若该程序运行后输出的值是
9
5
，判断框内“k＞a”，且a∈Z，则a=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网