题目内容
若函数f(x)的定义域内存在实数x,满足f(-x)=-f(x),则称f(x)为“局部奇函数”.例如:f(x)=x2+x-1在R上存在x=1,满足f(-1)=-f(1),故称f(x)=x2+x-1为“局部奇函数”.
(1)已知二次函数f(x)=ax2+2bx-4a(a,b∈R),试判断f(x)是否为“局部奇函数”,并说明理由;
(2)设f(x)=2x+m是定义在[-1,1]上的“局部奇函数”,求实数m的取值范围.
(1)已知二次函数f(x)=ax2+2bx-4a(a,b∈R),试判断f(x)是否为“局部奇函数”,并说明理由;
(2)设f(x)=2x+m是定义在[-1,1]上的“局部奇函数”,求实数m的取值范围.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)f(x)为“局部奇函数”等价于关于x的方程f(-x)+f(x)=0有解.解对应的方程,可得结论;
(2)若f(x)=2x+m是定义在[-1,1]上的“局部奇函数”,即方程2x+2-x+2m=0在[-1,1]上有解,利用换元法可求出实数m的取值范围.
(2)若f(x)=2x+m是定义在[-1,1]上的“局部奇函数”,即方程2x+2-x+2m=0在[-1,1]上有解,利用换元法可求出实数m的取值范围.
解答:
解:(1)f(x)为“局部奇函数”等价于关于x的方程f(-x)+f(x)=0有解.
f(-x)+f(x)=0,即2a(x2-4)=0 …(3分)
解得x=±2,
∴f(x)为“局部奇函数”…(5分)
(2)∵f(x)=2x+m,
∴f(-x)+f(x)=0可转化为2x+2-x+2m=0 …(8分)
∵f(x)=2x+m是定义在[-1,1]上的“局部奇函数”,
∴方程2x+2-x+2m=0在[-1,1]上有解,
令t=2x,(t∈[
,2],
∴-2m=t+
,…(9分)
∵g(t)=t+
在[
,1)上递减,在[1,2]上递增,
∴g(t)∈[2,
]…(11分)
∴-2m∈[2,
],
即m∈[-
,-1]…(13分)
f(-x)+f(x)=0,即2a(x2-4)=0 …(3分)
解得x=±2,
∴f(x)为“局部奇函数”…(5分)
(2)∵f(x)=2x+m,
∴f(-x)+f(x)=0可转化为2x+2-x+2m=0 …(8分)
∵f(x)=2x+m是定义在[-1,1]上的“局部奇函数”,
∴方程2x+2-x+2m=0在[-1,1]上有解,
令t=2x,(t∈[
| 1 |
| 2 |
∴-2m=t+
| 1 |
| t |
∵g(t)=t+
| 1 |
| t |
| 1 |
| 2 |
∴g(t)∈[2,
| 5 |
| 2 |
∴-2m∈[2,
| 5 |
| 2 |
即m∈[-
| 5 |
| 4 |
点评:本题考查的知识点是函数奇偶性的性质,其中正确理解“局部奇函数”的概念是解答的关键.

练习册系列答案
相关题目
cos(π+α)=( )
| A、cosα | B、-cosα |
| C、sinα | D、-sinα |
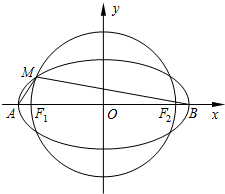 如图,在平面直角坐标系xOy中,椭圆
如图,在平面直角坐标系xOy中,椭圆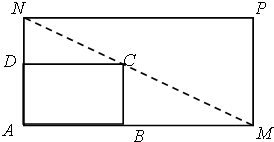 如图所示,将一矩形花坛ABCD扩建为一个更大的矩形花坛AMPN,要求点B在AM上,点D在AN上,且对角线MN过点C,已知AB=3米,AD=2米,当DN的长为多少时,矩形花坛AMPN的面积最小?并求出最小值.
如图所示,将一矩形花坛ABCD扩建为一个更大的矩形花坛AMPN,要求点B在AM上,点D在AN上,且对角线MN过点C,已知AB=3米,AD=2米,当DN的长为多少时,矩形花坛AMPN的面积最小?并求出最小值.