题目内容
已知函数f(x)=x2+2ax+1,g(x)=2x+2a(a∈R)
(1)若对任意x∈R,不等式f(x)≥
g(x)恒成立,求实数a的取值范围;
(2)设函数m(x)=
,求m(x)在x∈[2,4]上的最小值.
(1)若对任意x∈R,不等式f(x)≥
| 1 |
| 2 |
(2)设函数m(x)=
|
考点:二次函数的性质,二次函数在闭区间上的最值
专题:函数的性质及应用
分析:(1)根据一元二次不等式的性质可知,不等式f(x)≥
g(x)恒成立,对任意实数x恒成立等价于△=(2a-1)2-4(1-a)≤0,求解即可得实数m的取值范围;
(2)若2a-1=-1,即a=0时,f(x)-g(x)=x2+1-2x=(x-1)2≥0恒成立,此时f(x)≥g(x)恒成立,故此时m(x)=g(x)=2x;若2a-1≠-1,即a≠0时,f(x)-g(x)有两个零点1-2a,1,即f(x),g(x)的图象有两个交点,分类讨论m(x)在x∈[2,4]上的最小值,最后综合讨论结果,可得答案.
| 1 |
| 2 |
(2)若2a-1=-1,即a=0时,f(x)-g(x)=x2+1-2x=(x-1)2≥0恒成立,此时f(x)≥g(x)恒成立,故此时m(x)=g(x)=2x;若2a-1≠-1,即a≠0时,f(x)-g(x)有两个零点1-2a,1,即f(x),g(x)的图象有两个交点,分类讨论m(x)在x∈[2,4]上的最小值,最后综合讨论结果,可得答案.
解答:
解:(1)若不等式f(x)≥
g(x)恒成立,
即x2+(2a-1)x+(1-a)≥0恒成立,
即△=(2a-1)2-4(1-a)≤0,
即4a2-3≤0,
解得a∈[-
,
],
故实数a的取值范围为:[-
,
];
(2)f(x)-g(x)=x2+(2a-2)x+(1-2a)=[x+(2a-1)](x-1),
若2a-1=-1,即a=0时,
f(x)-g(x)=x2+1-2x=(x-1)2≥0恒成立,此时f(x)≥g(x)恒成立,
故此时m(x)=g(x)=2x,
由m(x)在x∈[2,4]上为增函数,故此时m(x)在x∈[2,4]上的最小值为m(2)=4;
若2a-1≠-1,即a≠0时,
f(x)-g(x)有两个零点1-2a,1,
即f(x),g(x)的图象有两个交点,如下图所示:
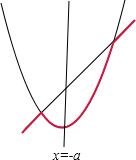
若1-2a<1,即a>0时,
m(x)在x∈[2,4]上为增函数,故此时m(x)在x∈[2,4]上的最小值为m(2)=g(2)=4+2a;
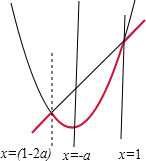
若1-2a>1,即a<0时,
当-a>4,即a<-4时,m(x)在x∈[2,4]上为减函数,
故此时m(x)在x∈[2,4]上的最小值为m(4)=f(4)=17+8a;
当2≤-a≤4,即-4≤a≤-2时,m(x)在x∈[2,-a]上为减函数,在x∈[-a,4]上为增函数,
故此时m(x)在x∈[2,4]上的最小值为m(-a)=f(-a)=1-a2;
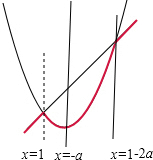
当-a<2<1-2a,即-2<a<-
时,m(x)在x∈[2,4]上为增函数,
故此时m(x)在x∈[2,4]上的最小值为m(2)=f(2)=5+4a;
当2≥1-2a,即-
≤a<0时,m(x)在x∈[2,4]上为增函数,
故此时m(x)在x∈[2,4]上的最小值为m(2)=g(2)=4+2a;
综上所述:m(x)在x∈[2,4]上的最小值为:
| 1 |
| 2 |
即x2+(2a-1)x+(1-a)≥0恒成立,
即△=(2a-1)2-4(1-a)≤0,
即4a2-3≤0,
解得a∈[-
| ||
| 2 |
| ||
| 2 |
故实数a的取值范围为:[-
| ||
| 2 |
| ||
| 2 |
(2)f(x)-g(x)=x2+(2a-2)x+(1-2a)=[x+(2a-1)](x-1),
若2a-1=-1,即a=0时,
f(x)-g(x)=x2+1-2x=(x-1)2≥0恒成立,此时f(x)≥g(x)恒成立,
故此时m(x)=g(x)=2x,
由m(x)在x∈[2,4]上为增函数,故此时m(x)在x∈[2,4]上的最小值为m(2)=4;
若2a-1≠-1,即a≠0时,
f(x)-g(x)有两个零点1-2a,1,
即f(x),g(x)的图象有两个交点,如下图所示:

若1-2a<1,即a>0时,

m(x)在x∈[2,4]上为增函数,故此时m(x)在x∈[2,4]上的最小值为m(2)=g(2)=4+2a;
若1-2a>1,即a<0时,

当-a>4,即a<-4时,m(x)在x∈[2,4]上为减函数,
故此时m(x)在x∈[2,4]上的最小值为m(4)=f(4)=17+8a;
当2≤-a≤4,即-4≤a≤-2时,m(x)在x∈[2,-a]上为减函数,在x∈[-a,4]上为增函数,
故此时m(x)在x∈[2,4]上的最小值为m(-a)=f(-a)=1-a2;
当-a<2<1-2a,即-2<a<-
| 1 |
| 2 |
故此时m(x)在x∈[2,4]上的最小值为m(2)=f(2)=5+4a;
当2≥1-2a,即-
| 1 |
| 2 |
故此时m(x)在x∈[2,4]上的最小值为m(2)=g(2)=4+2a;
综上所述:m(x)在x∈[2,4]上的最小值为:
|
点评:本题考查的知识点是二次函数的性质,二次函数在闭区间上的最值问题,(1)的关键是熟练掌握二次函数的图象和性质,(2)的关键是确定正确的分类标准.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
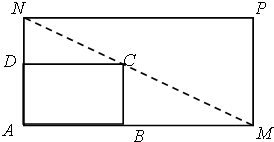 如图所示,将一矩形花坛ABCD扩建为一个更大的矩形花坛AMPN,要求点B在AM上,点D在AN上,且对角线MN过点C,已知AB=3米,AD=2米,当DN的长为多少时,矩形花坛AMPN的面积最小?并求出最小值.
如图所示,将一矩形花坛ABCD扩建为一个更大的矩形花坛AMPN,要求点B在AM上,点D在AN上,且对角线MN过点C,已知AB=3米,AD=2米,当DN的长为多少时,矩形花坛AMPN的面积最小?并求出最小值.