题目内容
比较下列各题中两个代数式的大小:
(1)当a>1时,a3与a2-a+1;
(2)
与1.
(1)当a>1时,a3与a2-a+1;
(2)
| 2x |
| x2+1 |
考点:不等式比较大小
专题:不等式的解法及应用
分析:利用做差法比价大小的是常用的方法,问题得以解决.
解答:
解:(1)a3-(a2-a+1)=(a-1)(a2+1),
因为a>1,所以a-1>0,a2+1>1,
所以a3-(a2-a+1)>0,
即a3>a2-a+1.
(2)
-1=
-
=
.
因为x2+1≥1,-(x-1)2≤0
所以
-1≤0
即
≤1
因为a>1,所以a-1>0,a2+1>1,
所以a3-(a2-a+1)>0,
即a3>a2-a+1.
(2)
| 2x |
| x2+1 |
| 2x |
| x2+1 |
| x2+1 |
| x2+1 |
| -(x-1)2 |
| x2+1 |
因为x2+1≥1,-(x-1)2≤0
所以
| 2x |
| x2+1 |
即
| 2x |
| x2+1 |
点评:本题主要考查了比较大小的常用方法,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 某几何体的三视图如图所示,设该几何体的体积为V1,半径为10的球的体积为V2,则V1:V2=( )
某几何体的三视图如图所示,设该几何体的体积为V1,半径为10的球的体积为V2,则V1:V2=( )| A、1:1 | B、1:2 |
| C、1:3 | D、1:4 |
cos(π+α)=( )
| A、cosα | B、-cosα |
| C、sinα | D、-sinα |
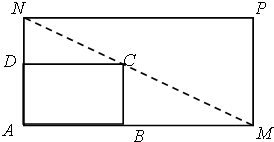 如图所示,将一矩形花坛ABCD扩建为一个更大的矩形花坛AMPN,要求点B在AM上,点D在AN上,且对角线MN过点C,已知AB=3米,AD=2米,当DN的长为多少时,矩形花坛AMPN的面积最小?并求出最小值.
如图所示,将一矩形花坛ABCD扩建为一个更大的矩形花坛AMPN,要求点B在AM上,点D在AN上,且对角线MN过点C,已知AB=3米,AD=2米,当DN的长为多少时,矩形花坛AMPN的面积最小?并求出最小值.