题目内容
已知AB是椭圆
+
=1(2010>b>0)的长轴,若把该长轴2010等分,过每个等分点作AB垂线,依次交椭圆的上半部分于P1,P2,…,P2009,F1为椭圆的左焦点,则
×(|F1A|+|F1P1|+|F1P2|+…+|F1P2009|+|F1B|)的值是 .
| x2 |
| 20102 |
| y2 |
| b2 |
| 1 |
| 2010 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:设P是任意一个等分点与椭圆
+
=1(2010>b>0)的交点,则必有一个与P对称的点P′,使得|PF1|+|P′F1|=|PF1|+|PF2|=2a=2×2010,这样的点共有2010对,包括A,B两点,由此能求出结果.
| x2 |
| 20102 |
| y2 |
| b2 |
解答:
 解:设P是任意一个等分点与椭圆
解:设P是任意一个等分点与椭圆
+
=1(2010>b>0)的交点,
则必有一个与P对称的点P′,
使得|PF1|+|P′F1|=|PF1|+|PF2|=2a=2×2010,
这样的点共有2010对,包括A,B两点,
∴
×(|F1A|+|F1P1|+|F1P2|+…+|F1P2009|+|F1B|)
=
×[(2×2010)×2010]
=2×2010
=4020.
故答案为:4020.
 解:设P是任意一个等分点与椭圆
解:设P是任意一个等分点与椭圆| x2 |
| 20102 |
| y2 |
| b2 |
则必有一个与P对称的点P′,
使得|PF1|+|P′F1|=|PF1|+|PF2|=2a=2×2010,
这样的点共有2010对,包括A,B两点,
∴
| 1 |
| 2010 |
=
| 1 |
| 2010 |
=2×2010
=4020.
故答案为:4020.
点评:本题考查椭圆性质的应用,是中档题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
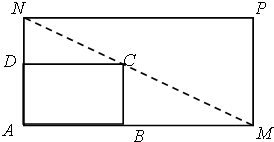 如图所示,将一矩形花坛ABCD扩建为一个更大的矩形花坛AMPN,要求点B在AM上,点D在AN上,且对角线MN过点C,已知AB=3米,AD=2米,当DN的长为多少时,矩形花坛AMPN的面积最小?并求出最小值.
如图所示,将一矩形花坛ABCD扩建为一个更大的矩形花坛AMPN,要求点B在AM上,点D在AN上,且对角线MN过点C,已知AB=3米,AD=2米,当DN的长为多少时,矩形花坛AMPN的面积最小?并求出最小值.