题目内容
已知
=(-4,6,-1),
=(4,3,-2),若|
|=1,且
⊥
,
⊥
,则
= .
| AB |
| AC |
| α |
| α |
| AB |
| α |
| AC |
| α |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:由于|
|=1,设
=(x,y,z),再由模的公式可得x2+y2+z2=1,运用向量的垂直条件:数量积为0,得到两个方程,解得即可.
| α |
| α |
解答:
解:由于|
|=1,设
=(x,y,z),
则x2+y2+z2=1,
由于
⊥
,
⊥
,
则-4x+6y-z=0,4x+3y-2z=0,
解得,x=
,y=
,z=
,或x=-
,y=-
,z=-
.
则有
=(
,
,
)或(-
,-
,-
).
故答案为:(
,
,
)或(-
,-
,-
).
| α |
| α |
则x2+y2+z2=1,
由于
| α |
| AB |
| α |
| AC |
则-4x+6y-z=0,4x+3y-2z=0,
解得,x=
| 3 |
| 13 |
| 4 |
| 13 |
| 12 |
| 13 |
| 3 |
| 13 |
| 4 |
| 13 |
| 12 |
| 13 |
则有
| α |
| 3 |
| 13 |
| 4 |
| 13 |
| 12 |
| 13 |
| 3 |
| 13 |
| 4 |
| 13 |
| 12 |
| 13 |
故答案为:(
| 3 |
| 13 |
| 4 |
| 13 |
| 12 |
| 13 |
| 3 |
| 13 |
| 4 |
| 13 |
| 12 |
| 13 |
点评:本题考查向量垂直的条件和模的定义,考查运算能力,属于基础题.

练习册系列答案
相关题目
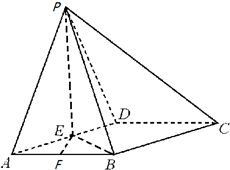 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为正三角形,且E,F分别为AD,AB的中点,PE⊥平面ABCD,BE⊥平面PAD.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为正三角形,且E,F分别为AD,AB的中点,PE⊥平面ABCD,BE⊥平面PAD. 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=