题目内容
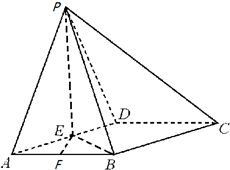 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为正三角形,且E,F分别为AD,AB的中点,PE⊥平面ABCD,BE⊥平面PAD.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为正三角形,且E,F分别为AD,AB的中点,PE⊥平面ABCD,BE⊥平面PAD.(Ⅰ)求证:BC⊥平面PEB;
(Ⅱ)求EF与平面PDC所成角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)证明:AD⊥平面PEB,利用四边形ABCD为菱形,可得AD∥BC,即可证明BC⊥平面PEB;
(Ⅱ)以E为原点,建立坐标系,求出平面PDC的法向量,利用向量的夹角公式,即可求EF与平面PDC所成角的正弦值.
(Ⅱ)以E为原点,建立坐标系,求出平面PDC的法向量,利用向量的夹角公式,即可求EF与平面PDC所成角的正弦值.
解答:
(Ⅰ)证明:∵PE⊥平面ABCD,BE⊥平面PAD,
∴PE⊥AD,BE⊥AD,
∵PE∩BE=EM,
∴AD⊥平面PEB,
∵四边形ABCD为菱形,
∴AD∥BC,
∴BC⊥平面PEB;
(Ⅱ)解:以E为原点,建立如图所示的坐标系,则

不妨设菱形ABCD的边长为2,则AE=ED=1,PA=2,PE=
,BE=
=
.
则点A(1,0,0),B(0,
,0),C(-2,
,0),D(-1,0,0),P(0,0,
),F(
,
,0).
=(-1,
,0),
=(1,0,
).
设平面PDC的法向量为
=(x,y,z).
则由
解得
不妨令z=1,得
=(-
,-1,1),
又
=(
,
,0),
所以EF与平面PDC所成角的正弦值为|
|=
.…(9分)
∴PE⊥AD,BE⊥AD,
∵PE∩BE=EM,
∴AD⊥平面PEB,
∵四边形ABCD为菱形,
∴AD∥BC,
∴BC⊥平面PEB;
(Ⅱ)解:以E为原点,建立如图所示的坐标系,则

不妨设菱形ABCD的边长为2,则AE=ED=1,PA=2,PE=
| 3 |
| AB2-AE2 |
| 3 |
则点A(1,0,0),B(0,
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| DC |
| 3 |
| DP |
| 3 |
设平面PDC的法向量为
| n |
则由
|
|
不妨令z=1,得
| n |
| 3 |
又
| EF |
| 1 |
| 2 |
| ||
| 2 |
所以EF与平面PDC所成角的正弦值为|
(-
| ||||||||
|
| ||
| 5 |
点评:本题主要考查了直线与平面垂直的判定,以及线面角及其度量,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
若函数f(x)的定义域是[0,2],则函数g(x)=
的定义域是( )
| f(2x) |
| x-1 |
| A、[0,2] |
| B、(1,2] |
| C、[0,1) |
| D、以上都不对 |
“a=1”是“行列式
=0”的( )
|
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
设f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则x•f(x)>0的解集是( )
| A、{x|-3<x<0,或x>3} |
| B、{x|x<-3,或0<x<3} |
| C、{x|x<-3,或x>3} |
| D、{x|-3<x<0,或0<x<3} |
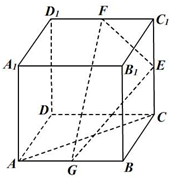 如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.