题目内容
已知抛物线Ω的顶点是坐标原点O,焦点F在y轴正半轴上,过点F的直线l与抛物线交于M、N两点且满足
•
=-3.
(1)求抛物线Ω的方程;
(2)若直线y=x与抛物线Ω交于A、B两点,在抛物线Ω上是否存在异于A,B的点C,使得经过A,B,C三点的圆和抛物线Ω在切点处有相同的切线?若存在,求出点C坐标;若不存在,请说明理由.
| OM |
| ON |
(1)求抛物线Ω的方程;
(2)若直线y=x与抛物线Ω交于A、B两点,在抛物线Ω上是否存在异于A,B的点C,使得经过A,B,C三点的圆和抛物线Ω在切点处有相同的切线?若存在,求出点C坐标;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)设抛物线方程为:x2=2py,焦点为(0,
),直线l:y=kx+
,联立抛物线方程,消去y,运用两根之积,再由向量的数量积的坐标公式,得到方程,解出即可;
(2)求出点A,B,假设抛物线L:x2=4y上存在点C(t,
)(t≠0且t≠4),使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线.设圆的圆心坐标为N(a,b),由圆的半径相等,得到a,b用t表示,
再由切线的斜率与导数的关系,及两直线垂直的关系,得到a,b,t的方程,再将a,b代入,得到t的方程,解出t,即可得到结论.
| p |
| 2 |
| p |
| 2 |
(2)求出点A,B,假设抛物线L:x2=4y上存在点C(t,
| t2 |
| 4 |
再由切线的斜率与导数的关系,及两直线垂直的关系,得到a,b,t的方程,再将a,b代入,得到t的方程,解出t,即可得到结论.
解答:
解:(1)设抛物线方程为:x2=2py,
焦点为(0,
),直线l:y=kx+
,
代入抛物线方程,得到x2-2pkx-p2=0,
设M(x1,y1),N(x2,y2),
则x1x2=-p2,yiy2=
•
=
,
由于
•
=-3,即有x1x2+y1y2=-3,
即有
-p2=-3,解得p=2,
即有抛物线方程为x2=4y;
(2)由y=x和抛物线方程.联立求得A(0,0),B(4,4).
假设抛物线L:x2=4y上存在点C(t,
)(t≠0且t≠4),
使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线.
设圆的圆心坐标为N(a,b),
∵
,∴
,
解得
,
∵抛物线L在点C处切线的斜率为k=y′|x=t=
,而t≠0,且该切线与NC垂直,
∴
•
=-1,即2a+bt-2t-
t3=0.
将
代入上式,得t3-2t2-8t=0.
即t(t-4)(t+2)=0.∵t≠0且t≠4,∴t=-2.
故满足题设的点C存在,其坐标为 (-2,1).
焦点为(0,
| p |
| 2 |
| p |
| 2 |
代入抛物线方程,得到x2-2pkx-p2=0,
设M(x1,y1),N(x2,y2),
则x1x2=-p2,yiy2=
| x12 |
| 2p |
| x22 |
| 2p |
| p2 |
| 4 |
由于
| OM |
| ON |
即有
| p2 |
| 4 |
即有抛物线方程为x2=4y;
(2)由y=x和抛物线方程.联立求得A(0,0),B(4,4).
假设抛物线L:x2=4y上存在点C(t,
| t2 |
| 4 |
使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线.
设圆的圆心坐标为N(a,b),
∵
|
|
解得
|
∵抛物线L在点C处切线的斜率为k=y′|x=t=
| t |
| 2 |
∴
b-
| ||
| a-t |
| t |
| 2 |
| 1 |
| 4 |
将
|
即t(t-4)(t+2)=0.∵t≠0且t≠4,∴t=-2.
故满足题设的点C存在,其坐标为 (-2,1).
点评:本题考查抛物线方程和性质,考查直线与抛物线的位置关系,考查抛物线的切线,考查学生的综合能力,难度较大.

练习册系列答案
相关题目
“a=1”是“行列式
=0”的( )
|
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
已知l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )
| A、若l⊥α,m?α,则l⊥m |
| B、若l⊥m,m?α,则l⊥α |
| C、若l∥α,m?α,则l∥m |
| D、若l∥α,m∥α,则l∥m |
用an表示正整数n的最大奇因数(如a3=3、a10=5),记数列{an}的前n项的和为Sn,则S64值为( )
| A、342 | B、1366 |
| C、2014 | D、5462 |
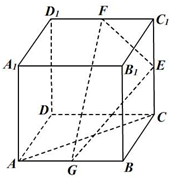 如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F,G分别为棱CC1,C1D1,AB的中点.