题目内容
四棱台两底面为矩形,底面对角线交点连线为棱台高12cm上底周长112cm,下底长宽分别为54cm,30cm 求侧面积.
考点:棱柱、棱锥、棱台的侧面积和表面积,棱台的结构特征
专题:空间位置关系与距离
分析:求出斜高运用侧面积公式即可得出答案.
解答:
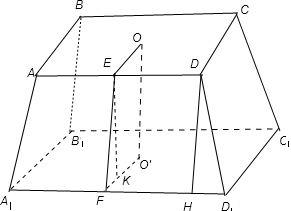 解:∵四棱台两底面为矩形,底面对角线交点连线为棱台高12cm上底周长112cm,下底长宽分别为54cm,30cm
解:∵四棱台两底面为矩形,底面对角线交点连线为棱台高12cm上底周长112cm,下底长宽分别为54cm,30cm
∴
=
,O′F=15
∴
=
,
∴KF=5,EK=12,
EF=13,
∴侧面积=
×(112+168)×13=1820
故侧面积为1820cm,
 解:∵四棱台两底面为矩形,底面对角线交点连线为棱台高12cm上底周长112cm,下底长宽分别为54cm,30cm
解:∵四棱台两底面为矩形,底面对角线交点连线为棱台高12cm上底周长112cm,下底长宽分别为54cm,30cm ∴
| 56 |
| 84 |
| 2 |
| 3 |
∴
| OE |
| O′F |
| 2 |
| 3 |
∴KF=5,EK=12,
EF=13,
∴侧面积=
| 1 |
| 2 |
故侧面积为1820cm,
点评:本题考查了空间几何体的性质,运算公式,属于计算题.

练习册系列答案
相关题目
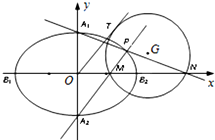 已知椭圆C:
已知椭圆C: