题目内容
17.在面积为S的正方形ABCD内任意投一点M,则点M到四边的距离均大于$\frac{{2\sqrt{S}}}{5}$的概率为( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{25}$ | D. | $\frac{4}{25}$ |
分析 由正方形面积求得边长,得到满足到四边的距离均大于$\frac{{2\sqrt{S}}}{5}$的点在以$\frac{\sqrt{S}}{5}$为边长的正方形区域内,求出点M所在区域面积,由面积比得答案.
解答 解:由正方形面积为S,可得边长为$\sqrt{S}$,
则满足到四边的距离均大于$\frac{{2\sqrt{S}}}{5}$的点在以$\frac{\sqrt{S}}{5}$为边长的正方形区域内.
所占区域面积为$(\frac{\sqrt{S}}{5})^{2}=\frac{S}{25}$.
由测度比为面积比可得点M到四边的距离均大于$\frac{{2\sqrt{S}}}{5}$的概率为$\frac{\frac{S}{25}}{S}=\frac{1}{25}$.
故选:C.
点评 本题考查几何概型,正确求出点M所在区域面积是关键,是中档题.

练习册系列答案
相关题目
12.下列函数中,在其定义域内既是奇函数又是增函数的是( )
| A. | y=-$\frac{1}{x}$ | B. | y=|x| | C. | y=x${\;}^{\frac{1}{3}}$ | D. | y=sinx |
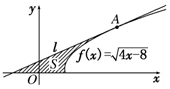 如图,过点A(6,4)作曲线f(x)=$\sqrt{4x-8}$的切线l.
如图,过点A(6,4)作曲线f(x)=$\sqrt{4x-8}$的切线l.