题目内容
7.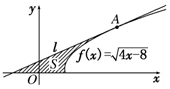 如图,过点A(6,4)作曲线f(x)=$\sqrt{4x-8}$的切线l.
如图,过点A(6,4)作曲线f(x)=$\sqrt{4x-8}$的切线l.(1)求切线l的方程;
(2)求切线l、x轴及曲线f(x)=$\sqrt{4x-8}$所围成的封闭图形的面积S.
分析 (1)利用导数的几何意义求出斜率,代入点斜式方程即可;
(2)根据定积分的几何意义求出面积.
解答 解:(1)f′(x)=$\frac{4}{2\sqrt{4x-8}}$=$\frac{1}{\sqrt{x-2}}$,
∴切线l的斜率k=f′(6)=$\frac{1}{2}$,
∴切线l的方程为y-4=$\frac{1}{2}$(x-6),即x-2y+2=0.
(2)l令f(x)=0得x=2,
把y=0代入x-2y+2=0得x=-2,
∴封闭图形的面积S=${∫}_{-2}^{6}$($\frac{1}{2}$x+1)dx-${∫}_{2}^{6}$$\sqrt{4x-8}$dx=($\frac{1}{4}$x2+x)${|}_{-2}^{6}$-$\frac{1}{6}$(4x-8)${\;}^{\frac{3}{2}}$${|}_{2}^{6}$=$\frac{16}{3}$.
点评 本题考查了导数的几何意义,定积分的几何意义,属于中档题.

练习册系列答案
相关题目
11.若实数x,y满足约束条件$\left\{\begin{array}{l}x-2y+3≥0\\ y≥x\\ x≥1\end{array}\right.$,则$z=\frac{y}{x+1}$的最小值为( )
| A. | $\sqrt{3}$ | B. | 1 | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
12.已知sin($\frac{π}{5}$-α)=$\frac{1}{4}$,则cos(2α+$\frac{3π}{5}$)=( )
| A. | -$\frac{7}{8}$ | B. | $\frac{7}{8}$ | C. | $\frac{1}{8}$ | D. | -$\frac{1}{8}$ |
2.已知函数$f(n)=\left\{{\begin{array}{l}{{n^2},n为奇数}\\{-{n^2},n为偶数}\end{array}}\right.$,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014=( )
| A. | -2013 | B. | -2014 | C. | 2013 | D. | 2014 |
12.函数$y=\frac{2tan3x}{{1+{{tan}^2}3x}}$的最小正周期是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | π |
16.若下列关于x的方程x2+4ax-4a+3=0(a为常数),x2+(a-1)x+a2=0,x2+2ax-2a=0中至少有一个方程有实根,则实数a的取值范围是( )
| A. | $({-\frac{3}{2},-1})$ | B. | $({-∞,-\frac{3}{2}}]∪[{-1,+∞})$ | C. | (-2,0) | D. | $({-∞,-\frac{3}{2}}]∪[{0,+∞})$ |
17.在面积为S的正方形ABCD内任意投一点M,则点M到四边的距离均大于$\frac{{2\sqrt{S}}}{5}$的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{25}$ | D. | $\frac{4}{25}$ |