题目内容
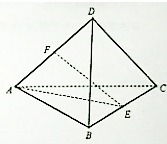 已知三棱锥D-ABC各棱长都相等(也称正四面体),E、F分别是BC、AD上的点.
已知三棱锥D-ABC各棱长都相等(也称正四面体),E、F分别是BC、AD上的点.(1)求证:直线AC与BD所成的角为90°;
(2)若E是BC的中点,求直线AE与BD所成角的余弦值;
(3)若AF:FD=CE:EB=3:2,设EF与AC、BD所成的角分别为α、β,求证:α+β=90°.
考点:直线与平面所成的角,棱锥的结构特征,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(1)取AC中点O,连接OD,OB,OD⊥AC,OB⊥AC,得出AC⊥面OBD,即可得证,
(2)根据向量运算
•
=
•(
-
)=
a×a×
-
a×a×
=-
,
得出cos<
,
>=
=-
,再用直线与直线的夹角求解.
(3)设棱长为5,作FM∥BD,连接ME,令FM=3,ME=2,运用向量得出EF=
,
运用勾股定理判断.
(2)根据向量运算
| AE |
| BD |
| AE |
| AD |
| AB |
| ||
| 2 |
| ||
| 3 |
| ||
| 2 |
| ||
| 2 |
| a2 |
| 4 |
得出cos<
| AE |
| BD |
-
| ||||
|
| ||
| 6 |
(3)设棱长为5,作FM∥BD,连接ME,令FM=3,ME=2,运用向量得出EF=
| 13 |
运用勾股定理判断.
解答:
证明:(1) 取AC中点O,连接OD,OB,
取AC中点O,连接OD,OB,
∵三棱锥D-ABC各棱长都相等(也称正四面体),E、F分别是BC、AD上的点.
∴OD⊥AC,OB⊥AC,
∵OB∩OD,
∴AC⊥面OBD,
∵DB?面OBD,
∴AC⊥BD,
即直线AC与BD所成的角为90,
(2)设棱长为a,
∴AE=
a,AD=a,AF=
,
=
-
,
∴
•
=
•(
-
)=
a×a×
-
a×a×
=-
,
∴cos<
,
>=
=-
,
∴直线AE与BD所成角的余弦值为
.
(3)设棱长为5,作FM∥BD,连接ME,
∴α=∠FEM,β=∠EFM
∵AF:FD=CE:EB=3:2,
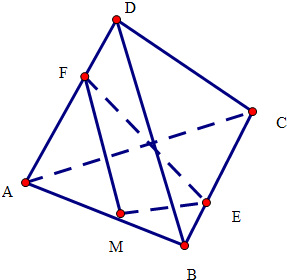
∴AF=3,FD=2,BE=2,EC=3,ME∥AC,
∴
═
,
=
,
∴FM=3,ME=2,
∵
=
-
=
+
-
,
∴(
)2=(
+
-
)2=
2+
2+
2+2
•
-2
•
-2
•
=9+25+4+2×5×2×(-
)-2×5×3×
-0=13,
∴EF=
,
∴△EFM中,FM=3,ME=2,EF=
,
∴EF2=FM2+ME2,
∴∠FME=
,
∠FEM+∠EFM=
∴α+β=90°
 取AC中点O,连接OD,OB,
取AC中点O,连接OD,OB,∵三棱锥D-ABC各棱长都相等(也称正四面体),E、F分别是BC、AD上的点.
∴OD⊥AC,OB⊥AC,
∵OB∩OD,
∴AC⊥面OBD,
∵DB?面OBD,
∴AC⊥BD,
即直线AC与BD所成的角为90,
(2)设棱长为a,
∴AE=
| ||
| 2 |
| a |
| 2 |
| BD |
| AD |
| AB |
∴
| AE |
| BD |
| AE |
| AD |
| AB |
| ||
| 2 |
| ||
| 3 |
| ||
| 2 |
| ||
| 2 |
| a2 |
| 4 |
∴cos<
| AE |
| BD |
-
| ||||
|
| ||
| 6 |
∴直线AE与BD所成角的余弦值为
| ||
| 6 |
(3)设棱长为5,作FM∥BD,连接ME,
∴α=∠FEM,β=∠EFM
∵AF:FD=CE:EB=3:2,

∴AF=3,FD=2,BE=2,EC=3,ME∥AC,
∴
| MF |
| BD |
| 3 |
| 5 |
| ME |
| AC |
| 2 |
| 5 |
∴FM=3,ME=2,
∵
| FE |
| AE |
| AF |
| AB |
| BE |
| AF |
∴(
| FE |
| AB |
| BE |
| AF |
| AF |
| AB |
| BE |
| AB |
| BE |
| AB |
| AF |
| BE |
| AF |
| 1 |
| 2 |
| 1 |
| 2 |
∴EF=
| 13 |
∴△EFM中,FM=3,ME=2,EF=
| 13 |
∴EF2=FM2+ME2,
∴∠FME=
| π |
| 2 |
∠FEM+∠EFM=
| π |
| 2 |
∴α+β=90°
点评:本题综合考查了运用向量的数量积,求解长度,夹角.解决空间直线的位置关系,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
某地消防大队紧急抽调1,2,3,4,5号五辆消防车,分配到附近的A,B,C,D四个村子进行送水抗旱工作,每个村子至少要安排一辆消防车,若这五辆消防车中去A村的辆数为随机变量ξ,则E(ξ)的值为( )
A、
| ||
B、
| ||
| C、1 | ||
D、
|
已知H是球O的直径AB上的一点,AH:HB=1:2,AH⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=lnx的定义域为(M,+∞),且M>0,且对任意,a,b,c∈(M,+∞),若a,b,c是直角三角形的三边长,且f(a),f(b),f(c)也能成为三角形的三边长,则M的最小值为( )
A、
| ||
B、2
| ||
C、3
| ||
| D、2 |
函数y=lg(kx2-2x+1)值域为R,则k的取值范围是( )
| A、(0,+∞) |
| B、(1,+∞) |
| C、(0,2) |
| D、[0,1] |