题目内容
过双曲线的右焦点F作实轴所在直线的垂线,交双曲线于A,B两点,设双曲线的左顶点为M,若点M在以AB为直径的圆的内部,则此双曲线的离心率e的取值范围为 .
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设双曲线的标准方程为:
-
=1(a>b>0).把x=c代入可得y=±
.由于左顶点M在以AB为直径的圆的内部,可得a+c<
,化简解出即可.
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
| b2 |
| a |
解答:
解:设双曲线的标准方程为:
-
=1(a>b>0).
把x=c代入可得y=±
.
∵左顶点M在以AB为直径的圆的内部,
∴a+c<
,∴a2+ac<c2-a2,
化为e2-e-2>0,
解得e>2.
则此双曲线的离心率e的取值范围为(2,+∞).
故答案为:(2,+∞).
| x2 |
| a2 |
| y2 |
| b2 |
把x=c代入可得y=±
| b2 |
| a |
∵左顶点M在以AB为直径的圆的内部,
∴a+c<
| b2 |
| a |
化为e2-e-2>0,
解得e>2.
则此双曲线的离心率e的取值范围为(2,+∞).
故答案为:(2,+∞).
点评:本题考查了双曲线与圆的标准方程及其性质,属于基础题.

练习册系列答案
相关题目
过点(4,-2)斜率为-
的直线的方程是( )
| ||
| 3 |
A、
| ||||
B、
| ||||
C、x+
| ||||
D、x+
|
已知数列{an}的通项an=
(n∈N*),则an取最大值时的n为( )
| 2n-5 |
| 2n |
| A、4 | B、12 | C、13 | D、不存在 |
函数f(x)=
的图象是( )
| 1 |
| |x+1| |
A、 |
B、 |
C、 |
D、 |
双曲线
-y2=1的离心率等于( )
| x2 |
| 4 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
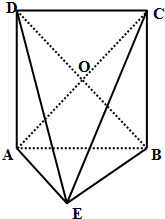 如图,在横放得四棱锥E-ABCD中,底面ABCD是正方形,∠DAE=90°,且△ABE是等腰直角三角形,其中∠BAE=90°,连接AC、BD交于点O.
如图,在横放得四棱锥E-ABCD中,底面ABCD是正方形,∠DAE=90°,且△ABE是等腰直角三角形,其中∠BAE=90°,连接AC、BD交于点O.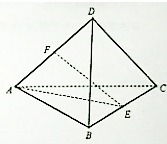 已知三棱锥D-ABC各棱长都相等(也称正四面体),E、F分别是BC、AD上的点.
已知三棱锥D-ABC各棱长都相等(也称正四面体),E、F分别是BC、AD上的点.