题目内容
若x＞0，y＞0，且满足4x+y=xy，则x+y的最小值为 ．
考点：基本不等式在最值问题中的应用
专题：不等式的解法及应用
分析：根据y=
，x＞1，x-1＞0，得出z=x+y=x+
，利用均值不等式求解．
| 4x |
| x-1 |
| 4x |
| x-1 |
解答：
解：∵x＞0，y＞0，且满足4x+y=xy，
∴y=
，x＞1，x-1＞0
∴z=x+y=x+
=（x-1）+
+5≥2
+5=9
（x=3时等号成立）
故答案为：9
∴y=
| 4x |
| x-1 |
∴z=x+y=x+
| 4x |
| x-1 |
| 4 |
| x-1 |
| 4 |
（x=3时等号成立）
故答案为：9
点评：本题考查了运用代入法解决两个变量的代数式的最值问题，利用基本不等式求解，注意变量的范围．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知数列{an}的通项an=
（n∈N*），则an取最大值时的n为（ ）
| 2n-5 |
| 2n |
| A、4 | B、12 | C、13 | D、不存在 |
双曲线
-y2=1的离心率等于（ ）
| x2 |
| 4 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
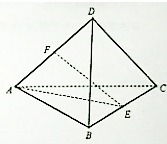已知三棱锥D-ABC各棱长都相等（也称正四面体），E、F分别是BC、AD上的点．