题目内容
已知H是球O的直径AB上的一点,AH:HB=1:2,AH⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:设球的半径为R,根据题意知由与球心距离为
R的平面截球所得的截面圆的面积是π,我们易求出截面圆的半径为1,根据球心距、截面圆半径、球半径构成直角三角形,满足勾股定理,我们易求出该球的半径,进而求出球的表面积.
| 1 |
| 3 |
解答:
解:设球的半径为R,∵AH:HB=1:2,∴平面α与球心的距离为
R,
∵α截球O所得截面的面积为π,
∴d=
R时,r=1,
故由R2=r2+d2得R2=12+(
R)2,∴R2=
∴球的表面积S=4πR2=
π.
故选:B.
| 1 |
| 3 |
∵α截球O所得截面的面积为π,
∴d=
| 1 |
| 3 |
故由R2=r2+d2得R2=12+(
| 1 |
| 3 |
| 9 |
| 8 |
∴球的表面积S=4πR2=
| 9 |
| 2 |
故选:B.
点评:本题考查的知识点是球的表面积公式,若球的截面圆半径为r,球心距为d,球半径为R,则球心距、截面圆半径、球半径构成直角三角形,满足勾股定理.

练习册系列答案
相关题目
双曲线
-y2=1的离心率等于( )
| x2 |
| 4 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
下列各组函数中,两个函数相等的是( )
A、f(x)=
| |||||||
B、f(x)=
| |||||||
C、f(x)=(
| |||||||
D、f(x)=
|
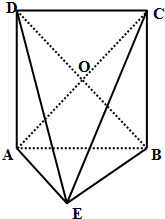 如图,在横放得四棱锥E-ABCD中,底面ABCD是正方形,∠DAE=90°,且△ABE是等腰直角三角形,其中∠BAE=90°,连接AC、BD交于点O.
如图,在横放得四棱锥E-ABCD中,底面ABCD是正方形,∠DAE=90°,且△ABE是等腰直角三角形,其中∠BAE=90°,连接AC、BD交于点O. 如图,海上有A,B两个小岛相距10km,船O将保持观望A岛和B岛所成的视角为60°,现从船O上派下一只小艇沿BO方向驶至C处进行作业,且OC=BO.设AC=xkm.
如图,海上有A,B两个小岛相距10km,船O将保持观望A岛和B岛所成的视角为60°,现从船O上派下一只小艇沿BO方向驶至C处进行作业,且OC=BO.设AC=xkm.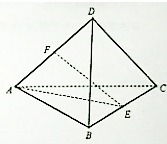 已知三棱锥D-ABC各棱长都相等(也称正四面体),E、F分别是BC、AD上的点.
已知三棱锥D-ABC各棱长都相等(也称正四面体),E、F分别是BC、AD上的点.