题目内容
点P在
-
=1上，若|PF1|=16，则|PF2|= ．
| x2 |
| 25 |
| y2 |
| 144 |
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：利用双曲线的定义和性质直接求解．
解答：
解：双曲线
-
=1中，
a=5，b=12，c=13，
设F1，F2分别为双曲线的左、右焦点，
∵|PF1|=16，
∴点P在双曲线的左支上，
根据双曲线的几何性质，得|PF2|-|PF1|=2a=10，
∴|PF2|=26．
故答案为：26．
| x2 |
| 25 |
| y2 |
| 144 |
a=5，b=12，c=13，
设F1，F2分别为双曲线的左、右焦点，
∵|PF1|=16，
∴点P在双曲线的左支上，
根据双曲线的几何性质，得|PF2|-|PF1|=2a=10，
∴|PF2|=26．
故答案为：26．
点评：本题考查双曲线的焦半径的求法，是基础题，解题时要认真审题，要熟练掌握双曲线的简单性质．
练习册系列答案
相关题目
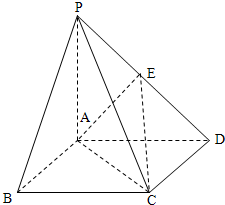如图，在四棱锥P-ABCD中，四边形ABCD为正方形，PA⊥面ABCD，且PA=AB=4，E为PD中点．
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|