题目内容
函数y=-x2+2x+1的值域为 ．
考点：函数的值域,函数的图象与图象变化
专题：常规题型,函数的性质及应用
分析：本题考查的是求二次函数的值域，常用的是用配方法来求．
解答：
解：y=-（x-1）2+2，在区间（-∞，1）上单调递增，在区间（1，+∞）上单调递减，
又f（1）=2，所以函数的值域为（-∞，2]．
故答案为：（-∞，2]．
又f（1）=2，所以函数的值域为（-∞，2]．
故答案为：（-∞，2]．
点评：在解题时要注意二次函数图象抛物线的开口方向，对称轴，在对称轴处取得最值．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
如图，在四棱锥P-ABCD中，底面ABCD是边长为1的菱形，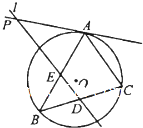
如图，△ABC内接于⊙O，过BC中点D作平行于AC的直线l，l交AB于E，交⊙O在A点处的切线于点P，若PE=6，ED=3，则AE的长为
如图，圆O是△ABC的外接圆，过点C作圆O的切线交BA的延长线于点D．若CD=已知集合A={x|-2≤x≤2}，B={x|0＜x＜1}，则有（ ）
| A、A＞B | B、A?B |
| C、B?A | D、A⊆B |