题目内容
已知直线l的参数方程为:
(t为参数),圆C的极坐标方程为ρ=2cosθ,则圆C的圆心到直线l的距离为 .
|
考点:直线的参数方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把直线l的参数方程和圆C的极坐标方程分别化为直角坐标方程,再利用点到直线的距离公式即可得出.
解答:
解:由直线l的参数方程为:
(t为参数),消去参数t得到y=2x+1.
由圆C的极坐标方程为ρ=2cosθ,
∴ρ2=2ρcosθ,化为x2+y2=2x,得到(x-1)2+y2=1,得到圆心(1,0),半径r=1.
∴圆C的圆心到直线l的距离d=
=
.
故答案为:
.
|
由圆C的极坐标方程为ρ=2cosθ,
∴ρ2=2ρcosθ,化为x2+y2=2x,得到(x-1)2+y2=1,得到圆心(1,0),半径r=1.
∴圆C的圆心到直线l的距离d=
| |2-0+1| | ||
|
3
| ||
| 5 |
故答案为:
3
| ||
| 5 |
点评:本题可查了查把参数方程和极坐标方程化为直角坐标方程、点到直线的距离公式,属于基础题.

练习册系列答案
相关题目

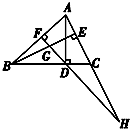 如图,AD、BE是△ABC的高,DF⊥AB于F,DF交BE于G,FD的延长线交AC的延长线于H,求证:DF2=FG•FH.
如图,AD、BE是△ABC的高,DF⊥AB于F,DF交BE于G,FD的延长线交AC的延长线于H,求证:DF2=FG•FH.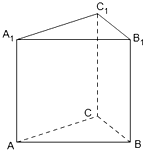 如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.
如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.