题目内容
已知向量
,
满足|
|=|
|=1,且
,
的夹角为
,O为平面直角坐标系的原点,点A、B满足
=2
+
,
=3
-
,则△OAB的面积为 .
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| OA |
| a |
| b |
| OB |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由向量的运算能求出|
|,|
|和
•
,代入夹角公式得cos∠BOA,利用三角函数知识能求出sin∠BOA,由此利用∴△OAB的面积S=
|
|•|
|•sin∠BOA,能求出结果.
| OA |
| OB |
| OA |
| OB |
| 1 |
| 2 |
| OA |
| OB |
解答:
解:∵向量
,
满足|
|=|
|=1,且
,
的夹角为
,
O为平面直角坐标系的原点,
点A、B满足
=2
+
,
=3
-
,
∴|
|=
=
=
=
,
|
|=
=
=
=
,
•
=(2
+
)•(3
-
)=6
2+
•
-
2=6+
-1=
,
∴cos∠BOA=
=
=
,
∴sin∠BOA=
=
,
∴△OAB的面积S=
|
|•|
|•sin∠BOA
=
×
×
×
=
.
故答案为:
.
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
O为平面直角坐标系的原点,
点A、B满足
| OA |
| a |
| b |
| OB |
| a |
| b |
∴|
| OA |
(2
|
4
|
4+4×
|
| 7 |
|
| OB |
(3
|
9
|
9-6×
|
| 7 |
| OA |
| OB |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
| 1 |
| 2 |
| 11 |
| 2 |
∴cos∠BOA=
| ||||
|
|
| ||||
|
| 11 |
| 14 |
∴sin∠BOA=
1-(
|
5
| ||
| 14 |
∴△OAB的面积S=
| 1 |
| 2 |
| OA |
| OB |
=
| 1 |
| 2 |
| 7 |
| 7 |
5
| ||
| 14 |
5
| ||
| 4 |
故答案为:
5
| ||
| 4 |
点评:本题考查三角形面积的求法,是中档题,解题题时要认真审题,注意向量的模、数量积、三角函数等知识点的合理运用.

练习册系列答案
相关题目
以下判断正确的是( )
| A、函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件 |
| B、命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” |
| C、命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
| D、“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
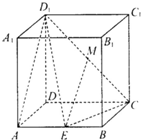 在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2.点E是线段AB上的动点,点M为D1C的中点.
在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2.点E是线段AB上的动点,点M为D1C的中点.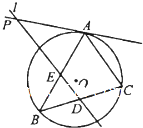 如图,△ABC内接于⊙O,过BC中点D作平行于AC的直线l,l交AB于E,交⊙O在A点处的切线于点P,若PE=6,ED=3,则AE的长为
如图,△ABC内接于⊙O,过BC中点D作平行于AC的直线l,l交AB于E,交⊙O在A点处的切线于点P,若PE=6,ED=3,则AE的长为