题目内容
已知△ABC面积S和三边a,b,c满足:S=a2-(b-c)2,b+c=8,则△ABC面积S的最大值为 .
考点:余弦定理
专题:三角函数的求值
分析:利用三角形面积公式变形出S,利用余弦定理列出关系式,代入已知等式计算即可求出S的最大值.
解答:
解:∵a2=b2+c2-2bccosA,即a2-b2-c2=-2bccosA,S△ABC=
bcsinA,
∴分别代入已知等式得:
bcsinA=2bc-2bccosA,即sinA=4-4cosA,
代入sin2A+cos2A=1得:cosA=
,
∴sinA=
,
∵b+c=8,
∴c=8-b,
∴S△ABC=
bcsinA=
bc=
b(8-b)≤
•(
)2=
,当且仅当b=8-b,即b=4时取等号,
则△ABC面积S的最大值为
.
故答案为:
| 1 |
| 2 |
∴分别代入已知等式得:
| 1 |
| 2 |
代入sin2A+cos2A=1得:cosA=
| 15 |
| 17 |
∴sinA=
| 8 |
| 17 |
∵b+c=8,
∴c=8-b,
∴S△ABC=
| 1 |
| 2 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 17 |
| b+8-b |
| 2 |
| 64 |
| 17 |
则△ABC面积S的最大值为
| 64 |
| 17 |
故答案为:
| 64 |
| 17 |
点评:此题考查了余弦定理,三角形的面积公式,以及同角三角函数间基本关系的运用,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
函数f(x)=
的值域是( )
|
| A、(0,+∞) | ||
| B、(0,1) | ||
C、[
| ||
D、[
|
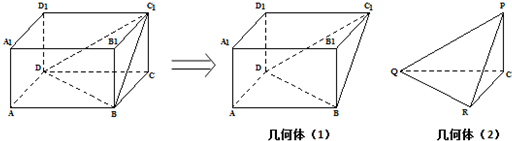
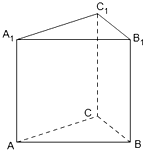 如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.
如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.