题目内容
函数y=x2-2x+3(-1≤x≤4)的值域为 .
考点:函数的值域
专题:函数的性质及应用
分析:本题考查的是二次函数在闭区间上的值域问题.
解答:
解:y=(x-1)2+2在区间[-1,1]上单调递减,在区间[1,4]上单调递增,
且f(-1)=6,f(1)=2,f(4)=11,
所以函数的值域为间[2,11].
故答案为;[2,11].
且f(-1)=6,f(1)=2,f(4)=11,
所以函数的值域为间[2,11].
故答案为;[2,11].
点评:对于二次函数在闭区间上的值域问题,可以先进行配方,再判断单调性求出最值,注意区间端点处的函数值.

练习册系列答案
相关题目
以下判断正确的是( )
| A、函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件 |
| B、命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” |
| C、命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 |
| D、“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
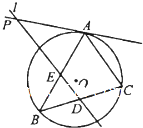 如图,△ABC内接于⊙O,过BC中点D作平行于AC的直线l,l交AB于E,交⊙O在A点处的切线于点P,若PE=6,ED=3,则AE的长为
如图,△ABC内接于⊙O,过BC中点D作平行于AC的直线l,l交AB于E,交⊙O在A点处的切线于点P,若PE=6,ED=3,则AE的长为 如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若CD=
如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若CD= 如图是一个从A→B的”闯关”游戏.规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于2n,则闯关成功.
如图是一个从A→B的”闯关”游戏.规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于2n,则闯关成功.