题目内容
20.已知$f(x)=2sinx•cos({x+\frac{π}{3}})+\frac{{\sqrt{3}}}{2}$.(1)求$f({-\frac{π}{4}})$的值;
(2)若$x∈[{0,\frac{π}{2}}]$,求f(x)的值域.
分析 由条件利用三角恒等变换化简函数f(x)的解析式,再利用正弦函数的定义域和值域求得f(x)的值域.
解答 解:(1)由于$f(x)=2sinx•cos({x+\frac{π}{3}})+\frac{{\sqrt{3}}}{2}=sinxcosx-\sqrt{3}{sin^2}x+\frac{{\sqrt{3}}}{2}=sin({2x+\frac{π}{3}})$.
∴$f({-\frac{π}{4}})=sin({-\frac{π}{6}})=-\frac{1}{2}$.
(2)∵$x∈[{0,\frac{π}{2}}]$,∴$2x+\frac{π}{3}∈[{\frac{π}{3},\frac{4π}{3}}]$,∴$f(x)∈[{-\frac{{\sqrt{3}}}{2},1}]$.
点评 本题主要考查三角恒等变换,正弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
10.已知函数f(x)=x2+2bx的图象在点A(0,f(0))处的切线l与直线x+y+3=0垂直,若数列{$\frac{1}{f(n)}$}的前n项和为Sn,则S2011的值为( )
| A. | $\frac{2012}{2011}$ | B. | $\frac{2010}{2011}$ | C. | $\frac{2013}{2012}$ | D. | $\frac{2011}{2012}$ |
15.设S是由任意n≥5个人组成的集合,如果S中任意4个人当中都至少有1个人认识其余3个人,那么,下面的判断中正确的是( )
| A. | S中没有人认识S中所有的人 | B. | S中至多有2人认识S中所有的人 | ||
| C. | S中至多有2人不认识S中所有的人 | D. | S中至少有1人认识S中的所有人 |
12.点A(sin2015°,cos2015°)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
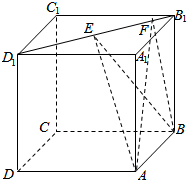 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中正确的序号是①②③.
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中正确的序号是①②③.