题目内容
11.若函数f(x),g(x)分别为R上的奇函数、偶函数,且满足f(x)-g(x)=ex.(1)求函数f(x)的解析式.
(2)求g(0)的值.
分析 (1)由题意用-x代替x,得f(-x)-g(-x)=e-x,利用f(x)、g(x)分别是R上的奇函数、偶函数,转化为关于f(x)和g(x)另外一个方程,再与已知方程联列,解之可得f(x),g(x)的解析式;
(2)由(1)中g(x)的解析式,将x=0代入可得答案.
解答 解:(1)∵f(x),g(x)分别为R上的奇函数,偶函数f(x)-g(x)=ex①
∴f(-x)-g(-x)=e-x
∴-f(x)-g(x)=e-x②
①-②得:f(x)=$\frac{1}{2}$(ex-e-x),
①+②得:g(x)=$\frac{1}{2}$(ex+e-x),
(2)g(0)=$\frac{1}{2}$(e0+e0)=1.
点评 本题考查的知识点函数奇偶性的性质,其中根据已知条件构造出第二个方程-f(x)+g(x)=e-x,是解答本题的关键.

练习册系列答案
相关题目
1.函数$y=2sin(\frac{π}{3}-x)-cos(\frac{π}{6}+x)(0≤x≤π)$的值域是( )
| A. | $[-1,\frac{{\sqrt{3}}}{2}]$ | B. | [-1,1] | C. | $[-\frac{{\sqrt{3}}}{2},\frac{{\sqrt{3}}}{2}]$ | D. | $[-\frac{{\sqrt{3}}}{2},1]$ |
19.下列命题错误的是( )
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0则x2+y2≠0”. | |
| B. | 若命题$p:?{x_0}∈R,x_0^2-{x_0}+1≤0$,则?p:?x∈R,x2-x+1>0. | |
| C. | △ABC中,sinA>sinB是A>B的充要条件. | |
| D. | ?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数. |
6.当且仅当 ,x2>2x>log2x.( )
| A. | 3<x<4 | B. | x>4 | C. | 0<x<2 | D. | 2<x<4 |
16.某几何体的三视图如图所示,则该几何体外接球的表面积为( )
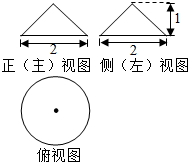

| A. | 4π | B. | π | C. | $\frac{π}{2}$ | D. | 2π |
3.$4{({\frac{16}{49}})^{-\frac{1}{2}}}+lg2+lg50$=( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |