题目内容

5．函数f（x）=lnx-|x-2|的零点的个数为2．

分析 函数f（x）=lnx-|x-2|的零点的个数，即函数y=lnx与函数y=|x-2|图象的交点个数，画出函数图象，数形结合，可得答案．

解答 解：函数f（x）=lnx-|x-2|的零点的个数，
即函数y=lnx与函数y=|x-2|图象的交点个数，
在同一坐标系中画出函数y=lnx与函数y=|x-2|图象如下图所示：

由图可得函数y=lnx与函数y=|x-2|图象有两个交点，
所以函数的零点个数为2，
故答案为：2

点评 本题考查的知识点是函数的零点，函数的图象．难度不大，属于基础题．

练习册系列答案
相关题目
15．函数y=sin2x+cos2x在[0，π]上的单调递减区间为[$\frac{π}{8}$，$\frac{5π}{8}$]．
16．某几何体的三视图如图所示，则该几何体外接球的表面积为（　　）
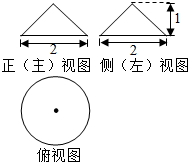
A．4πB．πC．$\frac{π}{2}$D．2π
13．若动点P（x，y）在$\frac{x^2}{4}+\frac{y^2}{9}=1$曲线上变化，则x2+2y的最大值为（　　）
A．$\frac{25}{4}$B．$\frac{27}{4}$C．6D．8
20．已知$f（x）=2sinx•cos（{x+\frac{π}{3}}）+\frac{{\sqrt{3}}}{2}$．
（1）求$f（{-\frac{π}{4}}）$的值；
（2）若$x∈[{0，\frac{π}{2}}]$，求f（x）的值域．
10．设等差数列{an}的前n项的和为Sn，且满足S2014＞0，S2015＜0，对任意正整数n，都有|an|≥|ak|，则k的值为1008．
17．已知函数f（x）=$\frac{1}{2}$x2-（a+$\frac{1}{a}$）x+lnx，其中a＞0．
（Ⅰ）当a=2时，求曲线y=f（x）在点（1，f（1））处切线的方程；
（Ⅱ）当a≠1时，求函数f（x）的单调区间；
（Ⅲ）若a∈（0，$\frac{1}{2}$），证明对任意x1，x2∈[$\frac{1}{2}$，1]（x1≠x2），$\frac{|f（{x}_{1}）-f（{x}_{2}）|}{{x}_{1}^{2}-{x}_{2}^{2}}$＜$\frac{1}{2}$恒成立．
14．如果椭圆$\frac{x^2}{81}+\frac{y^2}{25}=1$上一点M到此椭圆一个焦点F1的距离为10，N是MF1的中点，O是坐标原点，则ON的长为（　　）
A．2B．4C．8D．$\frac{3}{2}$
15．著名英国数学和物理学家Issac Newton（1643年-1727年）曾提出了物质在常温环境下温度变化的冷却模型．把物体放在冷空气中冷却，如果物体原来的温度是θ1℃，空气的温度是θ0℃，tmin后物体温度θ℃，可由公式θ=θ+（θ-θ）e-kt（e为自然对数的底数）得到，这里k是一个随着物体与空气的接触状况而定的正的常数．现将一个原来温度为62℃的物体放在15℃的空气中冷却，1min以后物体的温度是52℃．
（Ⅰ）求k的值（精确到0.01）；
（Ⅱ）该物体从原来的62℃开始冷却多少min后温度是32℃？
（参考数据：ln$\frac{37}{47}$≈-0.24，ln$\frac{27}{47}$≈-0.55，ln$\frac{17}{47}$≈-1.02）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网