题目内容
8.已知直线l:kx-y+1+2k=0.(k∈R).(1)若直线l不经过第四象限,求k的取值范围;
(2)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为4,求直线l的方程.
分析 (1)可求得直线l的方程及直线l在y轴上的截距,依题意则$\left\{\begin{array}{l}{k≥0}\\{1+2k≥0}\end{array}\right.$,从而可解得k的取值范围;
(2)依题意可求得A(-$\frac{1+2k}{k}$,0),B(0,1+2k),S△AOB=$\frac{1}{2}$(1+2k)$\frac{1+2k}{k}$=4,解得即可.
解答 解:(1)直线l的方程可化为:y=kx+2k+1,则直线l在y轴上的截距为2k+1,
要使直线l不经过第四象限,则$\left\{\begin{array}{l}{k≥0}\\{1+2k≥0}\end{array}\right.$,解得k的取值范围是:k≥0,
(2)依题意,直线l在x轴上的截距为:-$\frac{1+2k}{k}$,在y轴上的截距为1+2k,
∴A(-$\frac{1+2k}{k}$,0),B(0,1+2k),又-$\frac{1+2k}{k}$<0且1+2k>0,
∴k>0
∴S△AOB=$\frac{1}{2}$(1+2k)$\frac{1+2k}{k}$=4,解得$\frac{1}{2}$,
∴$\frac{1}{2}$x-y+1+1=0,即x-2y+4=0.
点评 本题考查恒过定点的直线,考查直线的一般式方程,考查直线的截距及三角形的面积,属于中档题.

练习册系列答案
相关题目
19.下列命题错误的是( )
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0则x2+y2≠0”. | |
| B. | 若命题$p:?{x_0}∈R,x_0^2-{x_0}+1≤0$,则?p:?x∈R,x2-x+1>0. | |
| C. | △ABC中,sinA>sinB是A>B的充要条件. | |
| D. | ?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数. |
16.某几何体的三视图如图所示,则该几何体外接球的表面积为( )
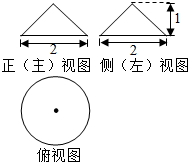

| A. | 4π | B. | π | C. | $\frac{π}{2}$ | D. | 2π |
3.$4{({\frac{16}{49}})^{-\frac{1}{2}}}+lg2+lg50$=( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
13.若动点P(x,y)在$\frac{x^2}{4}+\frac{y^2}{9}=1$曲线上变化,则x2+2y的最大值为( )
| A. | $\frac{25}{4}$ | B. | $\frac{27}{4}$ | C. | 6 | D. | 8 |