题目内容
17.已知y=f(x)+2x2是奇函数,且f(1)=2,若g(x)=f(x)+2x,则g(-1)=-8.分析 根据函数奇偶性的关系,建立方程关系进行求解即可.
解答 解:∵y=f(x)+2x2是奇函数,
∴设h(x)=f(x)+2x2,则h(-1)=-h(1),
则f(-1)+2=-[f(1)+2]=-4,
即f(-1)=-6,
∵g(x)=f(x)+2x,
∴g(-1)=f(-1)-2=-6-2=-8,
故答案为:-8
点评 本题主要考查函数值的计算,根据函数奇偶性的性质进行转化求解是解决本题的关键.

练习册系列答案
相关题目
9.已知函数f(x)=cos(sinx)+sin(cosx).则下列结论正确的是( )
| A. | f(x)的周期为π | B. | f(x)在(-$\frac{π}{2}$,0)上单调递减 | ||
| C. | f(x)的最大值为$\sqrt{2}$ | D. | f(x)的图象关于直线x=π对称 |
6.已知圆x2+y2=17在点(1,4)处的切线与幂函数f(x)的图象在点A(1,f(1))处的切线垂直,且不等式$\frac{f(x)}{x}$>ax2+x在(1,2)上能成立,则实数a的取值范围为( )
| A. | [0,+∞) | B. | ($\frac{35}{6}$,+∞) | C. | (-∞,0] | D. | (-∞,$\frac{3}{2}$) |
7.下列表述正确的是( )
| A. | 过平面β外一点可以作无数条直线与平面β平行 | |
| B. | 过直线l外一点可作无数条直线平行于l | |
| C. | 垂直于两条异面直线的空间直线只有一条 | |
| D. | 空间三个平面最多把空间分成七部分 |
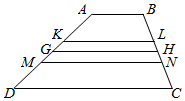 如图,四边形ABCD为梯形,其中AB=a,CD=b,若GH表示平行于两底且与它们等距离的线段(即梯形的中位线),KL表示平行于两底且使梯形ABLK与梯形KLCD相似的线段,MN表示平行于两底且将梯形ABCD分为面积相等的两个梯形的线段.
如图,四边形ABCD为梯形,其中AB=a,CD=b,若GH表示平行于两底且与它们等距离的线段(即梯形的中位线),KL表示平行于两底且使梯形ABLK与梯形KLCD相似的线段,MN表示平行于两底且将梯形ABCD分为面积相等的两个梯形的线段.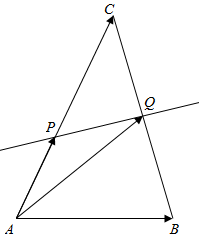 如图,已知△ABC的边BC的垂直平分线交AC于点P,交BC于点Q,若|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=5,则($\overrightarrow{AP}$+$\overrightarrow{AQ}$)•($\overrightarrow{AB}$-$\overrightarrow{AC}$)的值为-16.
如图,已知△ABC的边BC的垂直平分线交AC于点P,交BC于点Q,若|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=5,则($\overrightarrow{AP}$+$\overrightarrow{AQ}$)•($\overrightarrow{AB}$-$\overrightarrow{AC}$)的值为-16.