题目内容
8.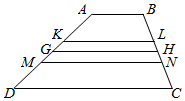 如图,四边形ABCD为梯形,其中AB=a,CD=b,若GH表示平行于两底且与它们等距离的线段(即梯形的中位线),KL表示平行于两底且使梯形ABLK与梯形KLCD相似的线段,MN表示平行于两底且将梯形ABCD分为面积相等的两个梯形的线段.
如图,四边形ABCD为梯形,其中AB=a,CD=b,若GH表示平行于两底且与它们等距离的线段(即梯形的中位线),KL表示平行于两底且使梯形ABLK与梯形KLCD相似的线段,MN表示平行于两底且将梯形ABCD分为面积相等的两个梯形的线段.试研究线段GH,KL,MN与代数式$\frac{a+b}{2}$,$\sqrt{ab}$,$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$之间的关系(需写出计算过程),并据此得到它们之间的一个大小关系.请你用基本不等式证明所得的结论.
分析 由相似及梯形的面积公式可得GH=$\frac{AB+CD}{2}$=$\frac{a+b}{2}$,KL=$\sqrt{AB•CD}$=$\sqrt{ab}$,MN=$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$,从而利用基本不等式及作差法比较大小.
解答 解:∵GH是梯形ABCD的中位线,
∴GH=$\frac{AB+CD}{2}$=$\frac{a+b}{2}$,
∵KL表示平行于两底且使梯形ABLK与梯形KLCD相似的线段,
∴$\frac{AB}{KL}$=$\frac{KL}{CD}$,
∴KL=$\sqrt{AB•CD}$=$\sqrt{ab}$,
∵MN表示平行于两底且将梯形ABCD分为面积相等的两个梯形的线段,
∴设梯形ABCD的高为h,则梯形ABNM的高为$\frac{MN-AB}{CD-AB}$h,
由题意知,
$\frac{1}{2}$$\frac{AB+MN}{2}$•$\frac{MN-AB}{CD-AB}$h=$\frac{1}{2}•$$\frac{1}{2}$$\frac{AB+CD}{2}$•h,
解得,MN=$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$,
由基本不等式可得,$\sqrt{ab}$≤$\frac{a+b}{2}$,
(当且仅当a=b时,等号成立),
故$\sqrt{ab}$<$\frac{a+b}{2}$,
$\frac{{a}^{2}+{b}^{2}}{2}$-($\frac{a+b}{2}$)2=$\frac{(a-b)^{2}}{4}$>0,
故$\frac{a+b}{2}$<$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$,
故$\sqrt{ab}$<$\frac{a+b}{2}$<$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$,
即KL<GH<MN.
点评 本题考查了梯形的性质的应用及基本不等式的应用,同时考查了数形结合的思想应用.

| A. | 2 | B. | 3 | C. | 9 | D. | 32 |
| A. | 2$\sqrt{2}$ | B. | $\sqrt{10}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
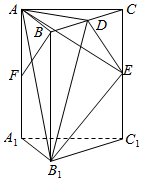 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=1,AC=$\sqrt{3}$,AA1=4,点D、E、F分别是棱BC、CC1、AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=1,AC=$\sqrt{3}$,AA1=4,点D、E、F分别是棱BC、CC1、AA1的中点. 如图,扇形的半径为r cm,周长为20cm,问扇形的圆心角α等于多少弧度时,这个扇形的面积最大,并求出扇形面积的最大值.
如图,扇形的半径为r cm,周长为20cm,问扇形的圆心角α等于多少弧度时,这个扇形的面积最大,并求出扇形面积的最大值.