题目内容
7.已知复数z=m2-2m-3+(m-3)i,其中m∈R.(1)若m=2,求$\overline{z}$+|z|;
(2)若z为纯虚数,求实数m的值.
分析 (1)利用复数的运算法则、共轭复数的定义、模的计算公式即可得出;
(2)利用纯虚数的定义即可得出.
解答 解:(1)m=2时,复数z=m2-2m-3+(m-3)i=-3-i.
∴$\overline{z}$=-3+i,|z|=$\sqrt{10}$.
∴$\overline{z}$+|z|=-3+i+$\sqrt{10}$=$\sqrt{10}$-3+i.
(2)∵z为纯虚数,
∴$\left\{\begin{array}{l}{{m}^{2}-2m-3=0}\\{m-3≠0}\end{array}\right.$,解得m=-1.
点评 本题考查了复数的运算法则、共轭复数的定义、模的计算公式、纯虚数的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知△ABC中,a=3,b=3$\sqrt{3}$,A=30°,则B等于( )
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
15.已知a∈R,那么“a>1”是“a2>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
2.已知函数f(x)=x2-3x,则$\underset{lim}{t→0}$$\frac{f(2)-f(2-3t)}{t}$的值为( )
| A. | -2 | B. | $\frac{1}{3}$ | C. | 1 | D. | 3 |
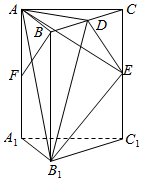 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=1,AC=$\sqrt{3}$,AA1=4,点D、E、F分别是棱BC、CC1、AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=1,AC=$\sqrt{3}$,AA1=4,点D、E、F分别是棱BC、CC1、AA1的中点. 如图,扇形的半径为r cm,周长为20cm,问扇形的圆心角α等于多少弧度时,这个扇形的面积最大,并求出扇形面积的最大值.
如图,扇形的半径为r cm,周长为20cm,问扇形的圆心角α等于多少弧度时,这个扇形的面积最大,并求出扇形面积的最大值.