题目内容
6．若圆C：x2+y2-2x+4y-20=0上有四个不同的点到直线l：4x+3y+c=0的距离为2，则c的取值范围是（ ）| A． | （-12，8） | B． | （-8，12） | C． | （-13，17） | D． | （-17，13） |
分析 由题意画出图形，若圆C：（x-1）2+（y+2）2=25有四个不同的点到直线l：4x+3y+c=0的距离为2，则圆心C（1，-2）到直线l的距离d＜3，由此列关于c的不等式得答案．
解答 解：圆C：x2+y2-2x+4y-20=0化为（x-1）2+（y+2）2=25，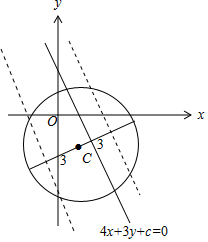
则圆心C为（1，-2），半径r=5．
若圆C：（x-1）2+（y+2）2=25有四个不同的点到直线l：4x+3y+c=0的距离为2，
则圆心C（1，-2）到直线l的距离d＜3，
如图：
即$\frac{|4×1+3×（-2）+c|}{5}$=$\frac{|c-2|}{5}$＜3，解得：-13＜c＜17，
∴c的取值范围是（-13，17）．
故选：C．
点评 本题考查直线与圆的位置关系，考查点到直线距离公式的应用，体现了数形结合的解题思想方法，是中档题．
练习册系列答案
启东小题作业本系列答案
相关题目
16．设点A（-1，2），B（2，3），C（3，-1），且$\overrightarrow{AD}=2\overrightarrow{AB}-3\overrightarrow{BC}$则点D的坐标为（ ）
| A． | .（2，16） | B． | .（-2，-16） | C． | .（4，16） | D． | （2，0） |
如图，在直三棱柱ABC-A1B1C1中，AB⊥侧面BB1C1C，AB1与A1B相交于点D，E是CC1上的点，且DE∥平面ABC，BC=1，BB1=2．
14．已知sin（π-α）＞0，且cos（π+α）＞0，则角α所在的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
1．
如图，在△ABC中，D为AB的中点，E为CD的中点，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，以向量$\overrightarrow{a}$，$\overrightarrow{b}$为基底，则向量$\overrightarrow{AE}$=（ ）
如图，在△ABC中，D为AB的中点，E为CD的中点，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，以向量$\overrightarrow{a}$，$\overrightarrow{b}$为基底，则向量$\overrightarrow{AE}$=（ ）| A． | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B． | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C． | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D． | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ |