题目内容
15.有N个人随机等可能地抢n(1≤n≤N)个红包,红包金额互不相同,且全部被抢光.(1)若每人最多可以抢一个红包,则有多少种结果?若每人可以抢多个红包,则有多少种结果?
(2)记“某指定的人恰好抢到k(k≤n)个红包”为事件Ak,求事件Ak的概率P(Ak);
(3)求某指定的人抢到的红包个数X的数学期望E(X),请写出推理过程.
分析 (1)若每人最多可以抢一个红包,则有${A}_{N}^{n}$种结果,若每人可以抢多个红包,则有Nn种结果.
(2)记“某指定的人恰好抢到k(k≤n)个红包”为事件Ak,利用等可能事件概率计算公式能求出事件Ak的概率.
(3)当n≥2时,kP(Ak)=$\frac{n}{N}{C}_{n-1}^{k-1}(1-\frac{1}{N})^{n-k}(\frac{1}{N})^{k-1}$,从而推导出E(X)=$\frac{n}{N}[(1-\frac{1}{N})+(\frac{1}{N})]^{n-1}$=$\frac{n}{N}$.当n=1时,E(X)=$\frac{1}{N}$,由此能求出结果.
解答 解:(1)若每人最多可以抢一个红包,则有${A}_{N}^{n}$种结果,
若每人可以抢多个红包,则有Nn种结果.
(2)记“某指定的人恰好抢到k(k≤n)个红包”为事件Ak,
则事件Ak的概率P(Ak)=$\frac{{C}_{n}^{k}(N-1)^{n-k}}{{N}^{n}}$.
(3)当n≥2时,kP(Ak)=$\frac{k{C}_{n}^{k}(N-1)^{n-k}}{{N}^{n}}$=$\frac{n{C}_{n-1}^{k-1}(N-1)^{n-k}}{{N}^{n}}$
=$\frac{n}{N}{C}_{n-1}^{k-1}\frac{(N-1)^{n-k}}{{N}^{(n+k)+(k-1)}}$=$\frac{n}{N}{C}_{n-1}^{k-1}(1-\frac{1}{N})^{n-k}(\frac{1}{N})^{k-1}$,
又E(X)=0×P(A0)+1×P(A1)+2×P(A2)+…+k×P(Ak)+…+n×P(An)
=$\frac{n}{N}$[${C}_{n-1}^{0}(1-\frac{1}{N})^{n-1}(\frac{1}{N})^{0}$+${C}_{n-1}^{1}(1-\frac{1}{N})^{n-2}(\frac{1}{N})$+…+${C}_{n-1}^{n-1}(1-\frac{1}{N})^{0}(\frac{1}{N})^{n-1}$]
=$\frac{n}{N}[(1-\frac{1}{N})+(\frac{1}{N})]^{n-1}$=$\frac{n}{N}$.
当n=1时,E(X)=$\frac{1}{N}$,
综上,E(X)=$\frac{n}{N}$.
点评 本题考查概率的求法,考查离散型随机变量的数学期望的求法,考查推理论证能力、运算求解能力,是中档题.

| A. | $\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B. | -$\frac{3}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{3}{2}$$\overrightarrow{b}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{3}{2}$$\overrightarrow{b}$ |
| A. | (-12,8) | B. | (-8,12) | C. | (-13,17) | D. | (-17,13) |
| A. | -$\frac{\sqrt{5}}{3}$ | B. | -$\frac{1}{9}$ | C. | $\frac{1}{9}$ | D. | $\frac{\sqrt{5}}{3}$ |
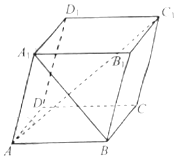 已知平行六面体ABCD-A1B1C1D1的底面ABCD为正方形,且∠A1AB=∠A1AD=60°,则当$\frac{{A}_{1}A}{AB}$=$\frac{\sqrt{17}-1}{4}$时,AC1⊥A1B.
已知平行六面体ABCD-A1B1C1D1的底面ABCD为正方形,且∠A1AB=∠A1AD=60°,则当$\frac{{A}_{1}A}{AB}$=$\frac{\sqrt{17}-1}{4}$时,AC1⊥A1B.