题目内容
1. 如图,在△ABC中,D为AB的中点,E为CD的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,以向量$\overrightarrow{a}$,$\overrightarrow{b}$为基底,则向量$\overrightarrow{AE}$=( )
如图,在△ABC中,D为AB的中点,E为CD的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,以向量$\overrightarrow{a}$,$\overrightarrow{b}$为基底,则向量$\overrightarrow{AE}$=( )| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ |
分析 利用向量的加减法运算法则,化简求解即可.
解答 解:因为E为CD的中点,则$\overrightarrow{AE}$=$\frac{1}{2}$($\overrightarrow{AD}$+$\overrightarrow{AC}$).因为D为AB的中点,则$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{AB}$.
所以$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AC}$,
故选:B.
点评 本题考查向量的四则运算,向量在几何中的应用,考查计算能力.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
11.在△ABC 中,a2=b2+c2+bc,则A等于( )
| A. | 60° | B. | 120° | C. | 30° | D. | 150° |
12. 如图,E,F分别是三棱锥P-ABC的棱AP,BC的中点,PC=AB=2,EF=$\sqrt{2}$,则异面直线AB与PC所成的角为( )
如图,E,F分别是三棱锥P-ABC的棱AP,BC的中点,PC=AB=2,EF=$\sqrt{2}$,则异面直线AB与PC所成的角为( )
 如图,E,F分别是三棱锥P-ABC的棱AP,BC的中点,PC=AB=2,EF=$\sqrt{2}$,则异面直线AB与PC所成的角为( )
如图,E,F分别是三棱锥P-ABC的棱AP,BC的中点,PC=AB=2,EF=$\sqrt{2}$,则异面直线AB与PC所成的角为( )| A. | 60° | B. | 45° | C. | 90° | D. | 30° |
16.对于非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,下列命题正确的是( )
| A. | 若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,则$\overrightarrow{b}$=$\overrightarrow{c}$, | B. | 若$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{c}$,则|$\overrightarrow{a}$|+|$\overrightarrow{b}$|>|$\overrightarrow{c}$| | ||
| C. | 若($\overrightarrow{a}$•$\overrightarrow{b}$)$\overrightarrow{c}$=0,则$\overrightarrow{a}$⊥$\overrightarrow{b}$ | D. | 若$\overrightarrow{a}$•$\overrightarrow{b}$>0,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为锐角 |
6.若圆C:x2+y2-2x+4y-20=0上有四个不同的点到直线l:4x+3y+c=0的距离为2,则c的取值范围是( )
| A. | (-12,8) | B. | (-8,12) | C. | (-13,17) | D. | (-17,13) |
1.设f(x)可导且下列各极限均存在,则( )成立.
| A. | $\underset{lim}{x→0}$$\frac{f(x)-f(0)}{x}$=f′(0) | B. | $\underset{lim}{h→0}$$\frac{f(a+2h)-f(a)}{h}$=f′(a) | ||
| C. | $\underset{lim}{△x→0}$$\frac{f({x}_{0})-f({x}_{0}-△x)}{△x}$=f′(x0) | D. | $\underset{lim}{△x→0}$$\frac{f({x}_{0}+△x)-f({x}_{0}-△x)}{2△x}$=f′(x0) |
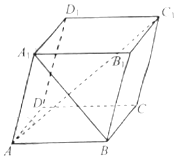 已知平行六面体ABCD-A1B1C1D1的底面ABCD为正方形,且∠A1AB=∠A1AD=60°,则当$\frac{{A}_{1}A}{AB}$=$\frac{\sqrt{17}-1}{4}$时,AC1⊥A1B.
已知平行六面体ABCD-A1B1C1D1的底面ABCD为正方形,且∠A1AB=∠A1AD=60°,则当$\frac{{A}_{1}A}{AB}$=$\frac{\sqrt{17}-1}{4}$时,AC1⊥A1B.