题目内容
14．已知sin（π-α）＞0，且cos（π+α）＞0，则角α所在的象限是（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 根据诱导公式化简即可判断．
解答 解：∵sinα=sin（π-α）＞0，
cosα=-cos（π+α）＜0，
则α是第二象限角，
故选：B．
点评 本题考查三角函数值的符号，牢记：一全正、二正弦、三正切、四余弦是解题的关键．
练习册系列答案
相关题目
4．
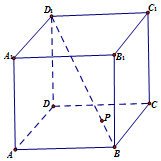正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$，动点P在对角线BD1上，过点P作垂直于BD1的平面α，平面α截正方体的表面得到一个多边形，记这样得到的截面多边形（含三角形）的周长为y，设BP=x，当$x∈[{\frac{1}{3}，\frac{5}{2}}]$时，函数y=f（x）的值域为（ ）
正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$，动点P在对角线BD1上，过点P作垂直于BD1的平面α，平面α截正方体的表面得到一个多边形，记这样得到的截面多边形（含三角形）的周长为y，设BP=x，当$x∈[{\frac{1}{3}，\frac{5}{2}}]$时，函数y=f（x）的值域为（ ）| A． | [1，3] | B． | [$\sqrt{6}$，3$\sqrt{6}$] | C． | [$\frac{3\sqrt{6}}{2}$，4$\sqrt{6}$] | D． | [$\sqrt{6}$，4$\sqrt{6}$] |
5．若向量$\overrightarrow{a}$=（1，1），$\overrightarrow{b}$=（1，-1），$\overrightarrow{c}$=（-1，2），则c=（ ）
| A． | $\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B． | -$\frac{3}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C． | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{3}{2}$$\overrightarrow{b}$ | D． | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{3}{2}$$\overrightarrow{b}$ |
如图，四棱锥P-ABCD中，底面ABCD是矩形，AD⊥PD，BC=1，PD=CD=2，∠PDC=120°．
19．$\frac{sin47°-sin13°}{sin17°}$的值为（ ）
| A． | $\sqrt{3}$ | B． | 1 | C． | -$\sqrt{3}$ | D． | -1 |
6．若圆C：x2+y2-2x+4y-20=0上有四个不同的点到直线l：4x+3y+c=0的距离为2，则c的取值范围是（ ）
| A． | （-12，8） | B． | （-8，12） | C． | （-13，17） | D． | （-17，13） |
4．已知sinα=$\frac{2}{3}$，α∈（$\frac{π}{2}$，$\frac{3π}{2}$），则cos（π-α）等于（ ）
| A． | -$\frac{\sqrt{5}}{3}$ | B． | -$\frac{1}{9}$ | C． | $\frac{1}{9}$ | D． | $\frac{\sqrt{5}}{3}$ |