题目内容
（1）已知：a，b，x均是正数，且a＜b，求证：
＞
；
（2）a，b，c是△ABC三边，证明：
+
+
＜2．
| a+x |
| b+x |
| a |
| b |
（2）a，b，c是△ABC三边，证明：
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
考点：不等式的证明
专题：不等式的解法及应用
分析：（1）利用不等式的基本性质，推出
＜1＜
，得到证明的结果；
（2）先根据三角形的三边关系及不等式的性质得出：
＜
=
，同理
＜
，
＜
，根据不等式的传递性即可证明．
| a |
| b |
| a+x |
| b+x |
（2）先根据三角形的三边关系及不等式的性质得出：
| a |
| b+c |
| a+a |
| b+c+a |
| 2a |
| a+b+c |
| b |
| a+c |
| 2b |
| a+b+c |
| c |
| a+b |
| 2c |
| a+b+c |
解答：
证明：（1）∵a＜b，∴
＜1，并且0＜a+x＜b+x，∴1＜
，
∴
＜1＜
，
即：
＞
．
（2）由“三角形两边之和大于第三边”可知，
，
，
，是正分数，
再利用（1）的结论可知：
＜
=
，
同理
＜
，
＜
，
根据不等式的可加性可知
+
+
=
+
+
=2．
∴a，b，c是△ABC三边，有
+
+
＜2成立．
| a |
| b |
| a+x |
| b+x |
∴
| a |
| b |
| a+x |
| b+x |
即：
| a+x |
| b+x |
| a |
| b |
（2）由“三角形两边之和大于第三边”可知，
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
再利用（1）的结论可知：
| a |
| b+c |
| a+a |
| b+c+a |
| 2a |
| a+b+c |
同理
| b |
| a+c |
| 2b |
| a+b+c |
| c |
| a+b |
| 2c |
| a+b+c |
根据不等式的可加性可知
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
| 2a |
| a+b+c |
| 2b |
| a+b+c |
| 2c |
| a+b+c |
∴a，b，c是△ABC三边，有
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
点评：本题主要考查不等式的证明，不等式的基本性质的应用，三角形的三边关系及不等式的性质．解题关键是运用不等式的传递性．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
设四边形ABCD内接于圆O，其对边AD与BC的延长线交于圆O外一点E，自E引一直线平行于AC，交BD延长线于点M，自M引MT切圆O于T点，则MT=ME．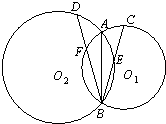
如图，假设两圆O1和O2交于A、B，⊙O1的弦BC交⊙O2于E，⊙O2的弦BD交⊙O1于F，证明：
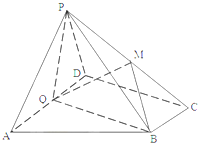如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD中点，M是棱PC上的点，PD=PA=2，BC=
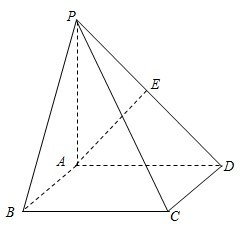如图，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，PA=AD，E为PD中点．