题目内容
在△ABC中,sinBcosC+sinCcosB=2sinAcosB,求sinA+sinC的取值范围.
考点:两角和与差的正弦函数
专题:三角函数的图像与性质
分析:由已知变形可得B=
,进而可得sinA+sinC=sinA+sin(
-A),由三角函数公式结合A的范围可求.
| π |
| 3 |
| 2π |
| 3 |
解答:
解:∵sinBcosC+sinCcosB=2sinAcosB,
∴sin(B+C)=2sinAcosB,
∴sinA=2sinAcosB,∴cosB=
,
∵B为三角形的内角,∴B=
,
∴sinA+sinC=sinA+sin(
-A)
=sinA+
cosA+
sinA
=
sinA+
cosA
=
(
sinA+
cosA)
=
sin(A+
),
∵A∈(0,
),
∴A+
∈(
,
),
∴sin(A+
)∈(
,1],
∴
sin(A+
)∈(
,
],
∴sinA+sinC∈(
,
],
∴sin(B+C)=2sinAcosB,
∴sinA=2sinAcosB,∴cosB=
| 1 |
| 2 |
∵B为三角形的内角,∴B=
| π |
| 3 |
∴sinA+sinC=sinA+sin(
| 2π |
| 3 |
=sinA+
| ||
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
| ||
| 2 |
=
| 3 |
| ||
| 2 |
| 1 |
| 2 |
=
| 3 |
| π |
| 6 |
∵A∈(0,
| 2π |
| 3 |
∴A+
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴sin(A+
| π |
| 6 |
| 1 |
| 2 |
∴
| 3 |
| π |
| 6 |
| ||
| 2 |
| 3 |
∴sinA+sinC∈(
| ||
| 2 |
| 3 |
点评:本题考查三角函数公式的应用,熟练应用公式是解决问题的关键,属中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
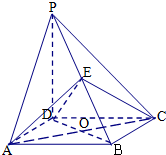 如图四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,点E在棱PB上.
如图四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,点E在棱PB上.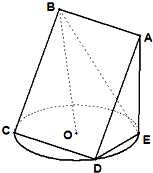 如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,正方形的边长为3
如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,正方形的边长为3