题目内容
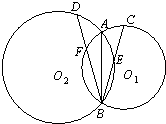如图，假设两圆O1和O2交于A、B，⊙O1的弦BC交⊙O2于E，⊙O2的弦BD交⊙O1于F，证明：（1）若∠DBA=∠CBA，则DF=CE；
（2）若DF=CE，则∠DBA=∠CBA．
考点：与圆有关的比例线段
专题：计算题,立体几何
分析：连接AC，AD，AE，AF，利用圆内接四边形，证明∠DAF=∠CAF
（1）证明△ADF≌△AEC，可得DF=CE；
（2）证明△ADF≌△AEC，可得AD=AE，即可证明∠DBA=∠CBA．
（1）证明△ADF≌△AEC，可得DF=CE；
（2）证明△ADF≌△AEC，可得AD=AE，即可证明∠DBA=∠CBA．
解答：
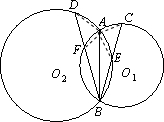证明：连接AC，AD，AE，AF，则
∵ADEB是圆内接四边形，
∴∠AEC=∠D，
同理∠C=∠AFD，
从而∠DAF=∠CAF
（1）∵∠DBA=∠CBA，
∴AD=AE，AF=AC，
∴△ADF≌△AEC，
∴DF=CE；
（2）∵DF=CE，
∴△ADF≌△AEC，
∴AD=AE，
∴∠DBA=∠CBA．
证明：连接AC，AD，AE，AF，则∵ADEB是圆内接四边形，
∴∠AEC=∠D，
同理∠C=∠AFD，
从而∠DAF=∠CAF
（1）∵∠DBA=∠CBA，
∴AD=AE，AF=AC，
∴△ADF≌△AEC，
∴DF=CE；
（2）∵DF=CE，
∴△ADF≌△AEC，
∴AD=AE，
∴∠DBA=∠CBA．
点评：本题考查圆内接四边形的性质，考查三角形全等的证明，正确运用圆内接四边形的性质是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
定义：称
为n个正数p1，p2，…，pn的“均倒数”，若数列{an}的前n项的“均倒数”为
，则数列{an}的通项公式为（ ）
| n |
| p1+p2+…+pn |
| 1 |
| 2n-1 |
| A、2n-1 | B、4n-3 |
| C、4n-1 | D、4n-5 |
