题目内容
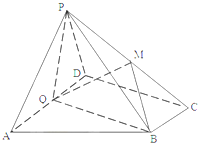如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD中点，M是棱PC上的点，PD=PA=2，BC=| 1 |
| 2 |
| 3 |
（1）若点M是棱PC的中点，求证：PA∥平面BMQ；
（2）求证：平面PQB⊥底面PAD；
（3）若二面角M-BQ-C大小为θ，且θ∈[
| π |
| 6 |
| π |
| 3 |
| PM |
| MC |
考点：与二面角有关的立体几何综合题,直线与平面平行的判定,平面与平面垂直的判定
专题：空间位置关系与距离
分析：（1）连结AC，交BQ于N，连结MN，由已知条件推导出四边形BCQA为平行四边形，且由此能证明PA∥平面MBQ．
（2）由已知条件推导出四边形BCDQ是平行四边形，从而得到QB⊥AD，由此能证明BQ⊥平面PAD，从而得到平面PQB⊥平面PAD．
（3）以Q为原点建立空间直角坐标系，利用向量法t的取值范围．
（2）由已知条件推导出四边形BCDQ是平行四边形，从而得到QB⊥AD，由此能证明BQ⊥平面PAD，从而得到平面PQB⊥平面PAD．
（3）以Q为原点建立空间直角坐标系，利用向量法t的取值范围．
解答：
（1）证明：连结AC，交BQ于N，连结MN，
∵BC=
AD=1，AD∥BC，Q为AD中点，
∴BC
AQ，∴四边形BCQA为平行四边形，且N为AC中点，
又∵点M是棱PC中点，∴MN∥PA，
∵MN?平面MQB，PA不包含于平面MQB，
∴PA∥平面MBQ．
（2）证明：∵AD∥BC，BC=
AD，Q为AD中点，
∴四边形BCDQ是平行四边形，
∴CD∥BQ，
∵∠ADC=90°，∴∠AQB=90°，∴QB⊥AD，
又∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，
∴BQ⊥平面PAD，
∵BQ?平面PQB，∴平面PQB⊥平面PAD．
（3）解：∵PA=PD，Q为AD的中点，∴PQ⊥AD，
∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，
∴PQ⊥平面ABCD，
如图，以Q为原点建立空间直角坐标系．
由题意知平面BQC的法向量为
=(0，0，1)，
Q（0，0，0），P（0，0，
），B（0，
，0），C（-1，
，0），
设M（x，y，z），
则
=(x，y，z-
)，
=(-1-x，
-y，-z)，
∵
=t
，∴
，∴
，
在平面MBQ中，
=(0，
，0)，
=(-
，
，
)，
设平面MBQ的法向量
=(x，y，z)，
则
，
取x=
，得
=(
，0，t)，
∵θ∈[
，
]，∴
=
∈[
，
]，解得，1≤t≤3，
∴t的取值范围为[1，3]．
∵BC=
| 1 |
| 2 |
∴BC
| ∥ |
. |
又∵点M是棱PC中点，∴MN∥PA，
∵MN?平面MQB，PA不包含于平面MQB，
∴PA∥平面MBQ．
（2）证明：∵AD∥BC，BC=
| 1 |
| 2 |
∴四边形BCDQ是平行四边形，
∴CD∥BQ，
∵∠ADC=90°，∴∠AQB=90°，∴QB⊥AD，
又∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，
∴BQ⊥平面PAD，
∵BQ?平面PQB，∴平面PQB⊥平面PAD．
（3）解：∵PA=PD，Q为AD的中点，∴PQ⊥AD，
∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，
∴PQ⊥平面ABCD，
如图，以Q为原点建立空间直角坐标系．
由题意知平面BQC的法向量为| n |
Q（0，0，0），P（0，0，
| 3 |
| 3 |
| 3 |
设M（x，y，z），
则
| PM |
| 3 |
| MC |
| 3 |
∵
| PM |
| MC |
|
|
在平面MBQ中，
| QB |
| 3 |
| QM |
| t |
| 1+t |
| ||
| 1+t |
| ||
| 1+t |
设平面MBQ的法向量
| m |
则
|
取x=
| 3 |
| m |
| 3 |
∵θ∈[
| π |
| 6 |
| π |
| 3 |
|
| ||||
|
|
| t | ||
|
| 1 |
| 2 |
| ||
| 2 |
∴t的取值范围为[1，3]．
点评：本题考查直线与平面平行的证明，考查平面与平面垂直的证明，考查实数的取值范围的求法，解题时要认真审题，注意向量法的合理运用．
练习册系列答案
相关题目
如图，正六边形ABCDEF中，已知