题目内容
△ABC的内角A、B、C的对边分别为a、b、c,已知a=
,b=
,B=45°,
(Ⅰ)求角A、C;
(Ⅱ)求边c.
| 3 |
| 2 |
(Ⅰ)求角A、C;
(Ⅱ)求边c.
考点:余弦定理,正弦定理
专题:解三角形
分析:(Ⅰ)由条件利用正弦定理求得sinA=
,可得A的值,再利用三角形内角和公式求得C的值.
(Ⅱ)由条件分类讨论,分别根据c=
计算求得结果.
| ||
| 2 |
(Ⅱ)由条件分类讨论,分别根据c=
| bsinC |
| sinB |
解答:
解:(Ⅰ)∵B=45°<90°且asinB<b<a,∴△ABC有两解.
由正弦定理得sinA=
=
=
,
则A为60°或120°.
(Ⅱ)①当A=60°时,C=180°-(A+B)=75°,
c=
=
=
.
②当A=120°时,C=180°-(A+B)=15°,
c=c=
═
=
.
故在△ABC中,A=60°,C=75°,c=
;
或A=120°,C=15°,c=
.
由正弦定理得sinA=
| asinB |
| b |
| ||
|
| ||
| 2 |
则A为60°或120°.
(Ⅱ)①当A=60°时,C=180°-(A+B)=75°,
c=
| bsinC |
| sinB |
| ||
| sin45° |
| ||||
| 2 |
②当A=120°时,C=180°-(A+B)=15°,
c=c=
| bsinC |
| sinB |
| ||
| sin45° |
| ||||
| 2 |
故在△ABC中,A=60°,C=75°,c=
| ||||
| 2 |
或A=120°,C=15°,c=
| ||||
| 2 |
点评:本题主要考查正弦定理、两角和的正弦公式,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形.将它沿AD折成大小为α(
如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形.将它沿AD折成大小为α(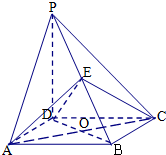 如图四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,点E在棱PB上.
如图四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,点E在棱PB上.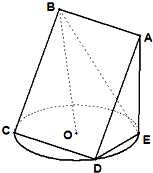 如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,正方形的边长为3
如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,正方形的边长为3 如图所示,已知圆O的直径AB=
如图所示,已知圆O的直径AB=