题目内容
5.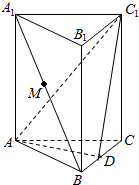 如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,AC=2$\sqrt{2}$,AA1=1,点D为BC的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,AC=2$\sqrt{2}$,AA1=1,点D为BC的中点.(1)求证:A1B∥平面ADC1
(2)设A1B的中点为M,求三棱锥M-AC1D的体积.
分析 (1)连结A1C交AC1于N,则DN为△A1BC的中位线,证出结论;
(2)V${\;}_{三棱锥M-A{C}_{1}D}$=$\frac{1}{2}$V${\;}_{三棱锥{B}_{1}-A{C}_{1}D}$.而V${\;}_{三棱锥{B}_{1}-A{C}_{1}D}$=V${\;}_{棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$-V${\;}_{三棱锥A-{A}_{1}{B}_{1}{C}_{1}}$-V${\;}_{三棱锥{B}_{1}-ABD}$-V${\;}_{三棱锥{C}_{1}-ACD}$=$\frac{1}{3}$V${\;}_{棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$,
解答 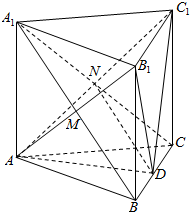 证明:(1)连结A1C交AC1于N,则DN为△A1BC的中位线,∴DN∥A1B,
证明:(1)连结A1C交AC1于N,则DN为△A1BC的中位线,∴DN∥A1B,
∵DN?平面ADC1,A1B?平面ADC1,
∴A1B∥平面ADC1
(2)∵AB=BC=2,AC=2$\sqrt{2}$,∴AB⊥BC,∴V${\;}_{棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{2}$AB•BC•AA1=2.
∵D是BC中点,∴V${\;}_{三棱锥{B}_{1}-ABD}$=V${\;}_{三棱锥{C}_{1}-ACD}$=$\frac{1}{6}$V${\;}_{棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$.
连结AB1,则M是AB1中点,∴V${\;}_{三棱锥M-A{C}_{1}D}$=$\frac{1}{2}$V${\;}_{三棱锥{B}_{1}-A{C}_{1}D}$.
∵V${\;}_{三棱锥{B}_{1}-A{C}_{1}D}$=V${\;}_{棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$-V${\;}_{三棱锥A-{A}_{1}{B}_{1}{C}_{1}}$-V${\;}_{三棱锥{B}_{1}-ABD}$-V${\;}_{三棱锥{C}_{1}-ACD}$=$\frac{1}{3}$V${\;}_{棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$,
∴V${\;}_{三棱锥M-A{C}_{1}D}$=$\frac{1}{6}$V${\;}_{棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{3}$.
点评 本题考查了线面平行的判定,几何体体积计算,当要求几何体体积不好直接求时,用作差法求体积是常用方法.


| A. | 21 | B. | -21 | C. | 15 | D. | 28 |
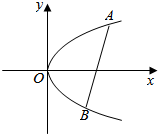 已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )| A. | 2p | B. | $\frac{5}{2}p$ | C. | $\frac{3}{2}p$ | D. | 3p |
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
| A. | 若|a|<|b|,则|a+c|<|b+c| | B. | 若|a|<|b|,则|a-c|<|b-c| | C. | 若|a|<|b-c|,则|a|<|b|-|c| | D. | 若|a|<|b-c|,则|a|-|c|<|b| |