题目内容
17．已知k∈N*，若曲线x2+y2=k2与曲线xy=k无交点，则k=1．分析 曲线x2+y2=k2与曲线xy=k联立，可得x4-k2x2+k2=0，利用△=0，求出k，结合k∈N*，若曲线x2+y2=k2与曲线xy=k无交点，即可求出k．
解答 解：曲线x2+y2=k2与曲线xy=k联立，可得x4-k2x2+k2=0
∴△=k4-4k2=0，
∴k=2，
∵k∈N*，若曲线x2+y2=k2与曲线xy=k无交点，
∴k=1．
故答案为：1．
点评 本题考查曲线与方程，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
7．函数f（x）=6-x-x2的单调递减区间是（ ）
| A． | $[-\frac{1}{2}，+∞）$ | B． | $[-\frac{1}{2}，2）$ | C． | $（-∞，-\frac{1}{2}]$ | D． | （-3，$-\frac{1}{2}]$ |
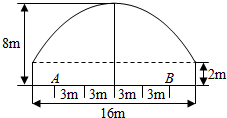有一隧道，内设双行线公路，同方向有两个车道（共有四个车道），每个车道宽为3m，此隧道的截面由一个长方形和一抛物线构成．如图所示，隧道高8m，宽16m，为了保证安全，要求行驶车辆顶部（设为平顶）与隧道顶部在竖直方面上高度之差至少为0.25m，靠近中轴线的车道为快车道，两侧的车道为慢车道，求车辆通过隧道时，慢车道的限制高度（用分数表示）．
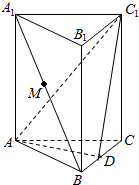如图，在直三棱柱ABC-A1B1C1中，AB=BC=2，AC=2$\sqrt{2}$，AA1=1，点D为BC的中点．