题目内容
14.已知直线l1:y=ax+1与l2:y=$\sqrt{3}$x+2互相垂直,则a=( )| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
分析 两直线互相垂直的充要条件是:k1k2=-1,由此建立关于a的方程,解之即可得到实数a的值.
解答 解:∵直线l1:y=ax+1与l2:y=$\sqrt{3}$x+2互相垂直,
∴$\sqrt{3}$a=-1,解之得a=-$\frac{\sqrt{3}}{3}$,
故选:D.
点评 本题给出两条直线互相垂直,求参数a之值,着重考查了平面直角坐标系中两条直线互相垂直的充要条件的知识,属于基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
19.在图中,U表示全集,用A、B表出阴影部分,其中表示正确的是( )


| A. | A∪B | B. | A∩B | C. | ∁U(A∩B) | D. | (∁UA)∩B |
3.任给△ABC,设角A,B,C所对的边分别为a,b,c,则下列等式成立的是( )
| A. | c2=a2+b2+2abcosC | B. | c2=a2+b2-2abcosC | ||
| C. | c2=a2+b2+2absinC | D. | c2=a2+b2-2absinC |
4.在等差数列{an}中,若a2=5,a10=21,则a6等于( )
| A. | 13 | B. | 15 | C. | 17 | D. | 48 |
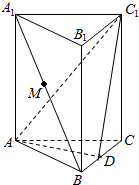 如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,AC=2$\sqrt{2}$,AA1=1,点D为BC的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,AC=2$\sqrt{2}$,AA1=1,点D为BC的中点.