题目内容
已知椭圆C1的方程为
+y2=1,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
(1)求双曲线C2的方程;
(2)若直线l:y=kx+
与双曲线C2恒有两个不同的交点A和B,且
•
>2(其中O为原点),求k的取值范围.
| x2 |
| 4 |
(1)求双曲线C2的方程;
(2)若直线l:y=kx+
| 2 |
| OA |
| OB |
考点:直线与圆锥曲线的综合问题
专题:计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析:(1)求出椭圆的焦点即为双曲线的顶点,椭圆的顶点即为双曲线的焦点,即有a=
,c=2,b=1.即可得到双曲线方程;
(2)联立直线方程和双曲线方程,消去y,得到x的方程,运用韦达定理和判别式大于0,再由向量的数量积的坐标运算,化简和整理得到k的不等式,解出求它们的交集即可.
| 3 |
(2)联立直线方程和双曲线方程,消去y,得到x的方程,运用韦达定理和判别式大于0,再由向量的数量积的坐标运算,化简和整理得到k的不等式,解出求它们的交集即可.
解答:
解:(1)椭圆C1的方程为
+y2=1的左、右焦点为(-
,0),(
,0),
则C2的左、右顶点为(-
,0),(
,0),
C1的左、右顶点为(-2,0),(2,0),则C2的左、右焦点为(-2,0),(2,0).
则双曲线的a=
,c=2,b=1.
即有双曲线C2的方程为:
-y2=1;
(2)将直线l:y=kx+
,与双曲线方程联立,消去y得,
(1-3k2)x2-6
kx-9=0
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
,
且1-3k2≠0,△=72k2+36(1-3k2)>0,即有k2≠
,k2<1.
由
•
>2得x1x2+y1y2=x1x2+(kx1+
)(kx2+
)
=(1+k2)x1x2+
k(x1+x2)+2>2,
即(1+k2)•
+
k•
>0,即
>0,
即有
<k2<3,又有k2≠
,k2<1.则有
<k2<1.
解得
<k<1或-1<k<-
.
故k的取值范围是(
,1)∪(-1,-
).
| x2 |
| 4 |
| 3 |
| 3 |
则C2的左、右顶点为(-
| 3 |
| 3 |
C1的左、右顶点为(-2,0),(2,0),则C2的左、右焦点为(-2,0),(2,0).
则双曲线的a=
| 3 |
即有双曲线C2的方程为:
| x2 |
| 3 |
(2)将直线l:y=kx+
| 2 |
(1-3k2)x2-6
| 2 |
设A(x1,y1),B(x2,y2),则x1+x2=
6
| ||
| 1-3k2 |
| -9 |
| 1-3k2 |
且1-3k2≠0,△=72k2+36(1-3k2)>0,即有k2≠
| 1 |
| 3 |
由
| OA |
| OB |
| 2 |
| 2 |
=(1+k2)x1x2+
| 2 |
即(1+k2)•
| -9 |
| 1-3k2 |
| 2 |
6
| ||
| 1-3k2 |
| 3(k2-3) |
| 1-3k2 |
即有
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解得
| ||
| 3 |
| ||
| 3 |
故k的取值范围是(
| ||
| 3 |
| ||
| 3 |
点评:本题考查椭圆、双曲线的方程和性质,考查联立直线方程和双曲线方程,消去未知数,运用韦达定理,考查向量的数量积的坐标运算,考查化简整理的运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
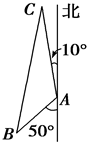 我舰在岛A南偏西50°相距12海里的B处发现敌舰正从岛A沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,求我舰航行速度.
我舰在岛A南偏西50°相距12海里的B处发现敌舰正从岛A沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,求我舰航行速度.