题目内容
已知等比数列{an}各项为正数,Sn是其前n项和,且a1+a5=34,a2•a4=64.求{an}的公比q及Sn.
考点:等比数列的前n项和,等比数列的通项公式
专题:等差数列与等比数列
分析:根据等比数列的性质和题意求出a1和a5,再分别由各项为正数求出q,由等比数列的前n项和公式求出Sn.
解答:
解:因为数列{an}是等比数列,所以a2•a4=a1•a5=64,
又因为a1+a5=34,所以a1和a5是方程x2-34x+64=0的两个根,
解得a1=2、a5=32,或a1=32、a5=2,
由an>0,当a1=2、a5=32时,
q4=
=16,得q=2,Sn=
=2n+1-2,
当a1=32、a5=2时,
q4=
=
,得q=
,Sn=
=64(1-
).
又因为a1+a5=34,所以a1和a5是方程x2-34x+64=0的两个根,
解得a1=2、a5=32,或a1=32、a5=2,
由an>0,当a1=2、a5=32时,
q4=
| a5 |
| a1 |
| 2(1-2n) |
| 1-2 |
当a1=32、a5=2时,
q4=
| a5 |
| a1 |
| 1 |
| 16 |
| 1 |
| 2 |
32[1-(
| ||
1-
|
| 1 |
| 2n |
点评:本题考查等比数列的性质,通项公式、前n项和公式的应用,熟练掌握公式是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
设等差数列{an}的前n项和为Sn,已知(1-a2012)3+2014(1-a2012)=2014,(a3-1)3+2014(a3-1)=2014,则下列结论正确的是( )
| A、S2014=2014,a2012<a3 |
| B、S2014=2014,a2012>a3 |
| C、S2014=2013,a2012<a3 |
| D、S2014=2013,a2012>a3 |
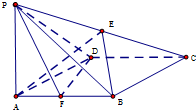 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.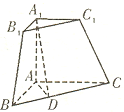 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,直线A1A⊥平面ABC,A1A=
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,直线A1A⊥平面ABC,A1A=