题目内容
梯形ABCD中,AD∥CP,PD⊥AD,CB⊥AD,∠DAC=
,PC=AC=2,如图①;现将其沿BC折成如图②的几何体,使得AD=
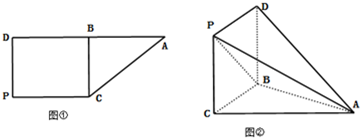
(Ⅰ)求直线BP与平面PAC所成角的正弦值;
(Ⅱ)求二面角C-PA-B的余弦值.
| π |
| 4 |
| 6 |

(Ⅰ)求直线BP与平面PAC所成角的正弦值;
(Ⅱ)求二面角C-PA-B的余弦值.
考点:用空间向量求平面间的夹角,直线与平面所成的角
专题:空间角
分析:(Ⅰ)由题意分别以BC、BA、BD所在直线为x轴、y轴、z轴,建立空间直角坐标系B-xyz,利用向量法能求出直线BP与平面PAC成的角.
(Ⅱ)求出平面PAB的法向量和平面PAC的法向量,利用向量法能求出二面角C-PA-B大小的余弦值.
(Ⅱ)求出平面PAB的法向量和平面PAC的法向量,利用向量法能求出二面角C-PA-B大小的余弦值.
解答:
 解:(Ⅰ)由题意,∵PC=AC=2,
解:(Ⅰ)由题意,∵PC=AC=2,
∴AB=BC=
,BD=2,AD=
.
在△ABD中,∵AB2+DB2=AD2,∴BD⊥BA,
∴BD、BA、BC两两垂直,
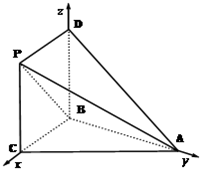
分别以BC、BA、BD所在直线为x轴、y轴、z轴,
建立空间直角坐标系B-xyz(如图).
A(0,
,0),B(0,0,0),C(
,0,0),P(
,0,2).
设平面PAC的法向量为
=(x,y,z),
=(-
,
,0),
=(0,0,2),
则
,取
=(1,1,0)
设直线BP与平面PAC成的角为θ,
则sinθ=|cps<
,
>|=
=
.
直线BP与平面PAC成的角为arcsin
.
(Ⅱ)设平面PAB的法向量为
=(a,b,c),
=(
,-
,2),
=(
,0,0).
=(0,-
,0),
=(
,-
,2).
由
,
令c=-1,∴
=(
,0,-1).
由(Ⅰ)知平面PAC的法向量为
=(1,1,0).
∴cos<
,
>=
=
,
由图知二面角C-PA-B为锐角,
∴二面角C-PA-B大小的余弦值为
.
 解:(Ⅰ)由题意,∵PC=AC=2,
解:(Ⅰ)由题意,∵PC=AC=2,∴AB=BC=
| 2 |
| 6 |
在△ABD中,∵AB2+DB2=AD2,∴BD⊥BA,
∴BD、BA、BC两两垂直,
分别以BC、BA、BD所在直线为x轴、y轴、z轴,
建立空间直角坐标系B-xyz(如图).
A(0,
| 2 |
| 2 |
| 2 |
设平面PAC的法向量为
| n |
| CA |
| 2 |
| 2 |
| CP |
则
|
| n |
设直线BP与平面PAC成的角为θ,
则sinθ=|cps<
| BP |
| n |
| ||||
|
| ||
| 6 |
直线BP与平面PAC成的角为arcsin
| ||
| 6 |
(Ⅱ)设平面PAB的法向量为
| m |
| AP |
| 2 |
| 2 |
| BC |
| 2 |
| AB |
| 2 |
| AP |
| 2 |
| 2 |
由
|
令c=-1,∴
| m |
| 2 |
由(Ⅰ)知平面PAC的法向量为
| n |
∴cos<
| m |
| n |
| ||||
|
| ||
| 3 |
由图知二面角C-PA-B为锐角,
∴二面角C-PA-B大小的余弦值为
| ||
| 3 |
点评:本题考查直线与平面所成角的正弦值的求法,考查二面角的余弦值的求法,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
已知简谐振动f(x)=Asin(ωx+φ)(|φ|<
)的振幅为
,图象上相邻最高点与最低点之间的距离为5,且过点(0,
),则该简谐振动的频率与初相分别为( )
| π |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知
=(a,-2),
=(1,1-a),则“a=2”是“
∥
”的( )
| m |
| n |
| m |
| n |
| A、充要条件 |
| B、充分而不必要条件 |
| C、必要而不充分条件 |
| D、既不充分也不必要条件 |
数列{an}满足a1=1,且an=
an-1+(
)n(n≥2,且n∈N*),则{an}的通项公式为( )
| 1 |
| 3 |
| 1 |
| 3 |
A、
| ||
B、
| ||
| C、n+2 | ||
| D、(n+2)3n |
设等差数列{an}的前n项和为Sn,已知(1-a2012)3+2014(1-a2012)=2014,(a3-1)3+2014(a3-1)=2014,则下列结论正确的是( )
| A、S2014=2014,a2012<a3 |
| B、S2014=2014,a2012>a3 |
| C、S2014=2013,a2012<a3 |
| D、S2014=2013,a2012>a3 |